Question

6．定义：有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形．
（Ⅰ）如图①，已知A，B，C在格点（小正方形的顶点）上，请在图①中画出一个以格点为顶点，AB，BC为边的对等四边形ABCD；
（2）如图②，在Rt△PBC中，∠PCB=90°，BC=11，tan∠PBC=$\frac{12}{5}$，点A在BP边上，且AB=13．点D在PC边上，且四边形ABCD为对等四边形，则CD的长为13、12-$\sqrt{85}$或12+$\sqrt{85}$．

Answer 1

分析 （1）根据对等四边形的定义，进行画图即可；
（2）根据对等四边形的定义，分两种情况：①若CD=AB，此时点D在D₁的位置，CD₁=AB=13；②若AD=BC=11，此时点D在D₂、D₃的位置，AD₂=AD₃=BC=11；利用勾股定理和矩形的性质，求出相关相关线段的长度，即可解答．

解答 解：（1）如图1所示（画2个即可）．
；

（2）如图2，点D的位置如图所示：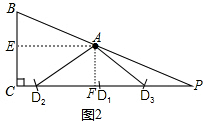

①若CD=AB，此时点D在D₁的位置，CD₁=AB=13；
②若AD=BC=11，此时点D在D₂、D₃的位置，AD₂=AD₃=BC=11，
过点A分别作AE⊥BC，AF⊥PC，垂足为E，F，
设BE=x，
∵tan∠PBC=$\frac{12}{5}$，
∴AE=$\frac{12}{5}$，
在Rt△ABE中，AE²+BE²=AB²，
即x²+（$\frac{12}{5}$x）²=13²，
解得：x₁=5，x₂=-5（舍去），
∴BE=5，AE=12，
∴CE=BC-BE=6，
由四边形AECF为矩形，可得AF=CE=6，CF=AE=12，
在Rt△AFD₂中，FD₂=$\sqrt{{AD}_{2}^{2}-A{F}^{2}}$=$\sqrt{85}$，
∴CD₂=CF-FD₂=12-$\sqrt{85}$，
CD₃=CF+FD₂=12+$\sqrt{85}$，
综上所述，CD的长度为13、12-$\sqrt{85}$或12+$\sqrt{85}$．
故答案为：13、12-$\sqrt{85}$或12+$\sqrt{85}$．

点评 本题主要考查了四边形的综合题，解题的关键是理解并能运用“等对角四边形”这个概念．在（2）中注意分类讨论思想的应用、勾股定理的应用．