
【题目】已知函数y=ax2-2ax-1(a是常数,a≠0),下列结论正确的是( )
A. 当a=1时,函数图象过点(-1,1)
B. 当a=-2时,函数图象与x轴没有交点
C. 若a>0,则当x≥1时,y随x的增大而减小
D. 若a<0,则当x≤1时,y随x的增大而增大
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
【题目】某市居民使用自来水按如下标准收费(水费按月缴纳)
户月用水量 | 单价 |
不超过 | 2元/ |
超过 | 3元/ |
超过 | 4元/ |
(1)某用户一个月用了![]() 水,则该用户缴纳的水费是______元;
水,则该用户缴纳的水费是______元;
(2)某户月用水量为![]() 立方米(10<x≤20),该用户缴纳的水费是______元(用含
立方米(10<x≤20),该用户缴纳的水费是______元(用含![]() 的整式表示)
的整式表示)
(3)一月份甲、乙两用户共用水![]() ,设甲用户用水量为
,设甲用户用水量为![]() ,且
,且![]() ,若他们这个月共付水费105元,求
,若他们这个月共付水费105元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
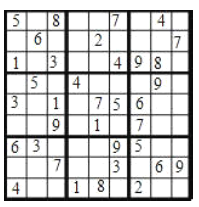
【题目】如图,一个![]() 的方格图,由粗线隔为
的方格图,由粗线隔为![]() 个横竖各有
个横竖各有![]() 个格的“小九宫”格,其中,有一些方格填有
个格的“小九宫”格,其中,有一些方格填有![]() 至
至![]() 的数字,小鸣在第九行的空格中各填入了一个不大于
的数字,小鸣在第九行的空格中各填入了一个不大于![]() 的正整数,使每行、每列和每个“小九宫”格内的数字都不重复,然后小鸣将第九行的数字从左向右写成一个
的正整数,使每行、每列和每个“小九宫”格内的数字都不重复,然后小鸣将第九行的数字从左向右写成一个![]() 位数,这个
位数,这个![]() 位数是 __________.
位数是 __________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长和宽分别是a,b的长方形的四个角都剪去一个边长为x的正方形,折叠后,做成一无盖的盒子(单位:cm).
(1)用a,b,x表示纸片剩余部分的面积;
(2)用a,b,x表示盒子的体积;
(3)当a=10,b=8且剪去的每一个小正方形的面积等于4 cm2时,求剪去的每一个正方形的边长及所做成的盒子的体积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(3)班数学兴趣小组经过市场调查整理发现某种商品的销售量P(件)与销售时间x天(1≤x≤90,且x为整数)成一次函数关系,具体数量关系如下表.已知商品的进价为30元/件,该商品的售价y(元/件)与销售时间x天的函数关系如图所示,每天的销售利润为w(元).
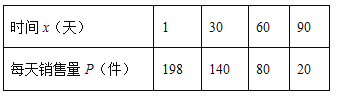
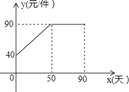
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0),B(1,0),直线x=-0.5与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC,BC,AD,BD,某同学根据图象写出下列结论:①a-b=0;②当-2<x<1时,y>0;③四边形ACBD是菱形;④9a-3b+c>0,你认为其中正确的是( )
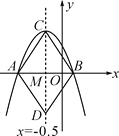
A. ②③④B. ①②④C. ①③④D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实素质教育要求,促进学生全面发展,我市某中学2016年投资11万元新增一批电脑,计划以后每年以相同的增长率进行投资,2018年投资18.59万元.
(1)求该学校为新增电脑投资的年平均增长率;
(2)从2016年到2018年,该中学三年为新增电脑共投资多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年巴西里约奥运会上,中国女排克服重重困难,凭借顽强的毅力和超强的实力先后战胜了实力同样超强的巴西队,荷兰队和塞尔维亚队,获得了奥运冠军,为祖国和人民争了光.
如图,已知女排球场的长度OD为18米,位于球场中线处的球网AB的高度为2.24米,一队员站在点O处发球,排球从点O的正上方2米的C点向正前方飞去,排球的飞行路线是抛物线的一部分,当排球运行至离点O的水平距离OE为6米时,到达最高点F,以O为原点建立如图所示的平面直角坐标系.
(1)当排球运行的最大高度为2.8米时,求排球飞行的高度y(单位:米)与水平距离x(单位:米)之间的函数关系式.
(2)在(1)的条件下,这次所发的球能够过网吗?如果能够过网,是否会出界?请说明理由.
(3)喜欢打排球的李明同学经研究后发现,发球要想过网,球运行的最大高度h(米)应满足h>2.32,但是他不知道如何确定h的取值范围,使排球不会出界(排球压线属于没出界),请你帮忙解决并指出使球既能过网又不会出界的h的取值范围 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上每相邻两点间的距离为一个单位长度,点![]() 、
、![]() 、
、![]() 、
、![]() 对应的数分别是
对应的数分别是![]() ,且
,且![]() .
.
(1)那么![]() ,
,![]() :
:
(2)点![]() 以
以![]() 个单位/秒的速度沿着数轴的正方向运动,
个单位/秒的速度沿着数轴的正方向运动,![]() 秒后点
秒后点![]() 以
以![]() 个单位/秒的速度也沿着数轴的正方向运动,当点
个单位/秒的速度也沿着数轴的正方向运动,当点![]() 到达点
到达点![]() 处立刻返回,与点
处立刻返回,与点![]() 在数轴的某点处相遇,求这个点对应的数;
在数轴的某点处相遇,求这个点对应的数;
(3)如果![]() 、
、![]() 两点以(2)中的速度同时向数轴的负方向运动,点
两点以(2)中的速度同时向数轴的负方向运动,点![]() 从图上的位置出发也向数轴的负方向运动,且始终保持
从图上的位置出发也向数轴的负方向运动,且始终保持![]() ,当点
,当点![]() 运动到
运动到![]() 时,点
时,点![]() 对应的数是多少?
对应的数是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com