
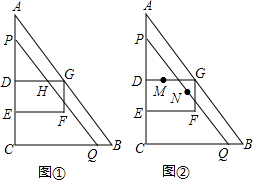
���� ��1���ɡ�ADG�ס�ACB���DG�����ɡ�PDH��ADG�����DH�����ɣ�
��2�����Ķε�0��t��2ʱ����2��t��4ʱ����4��t��6ʱ����6��t��8ʱ�ֱ����������ɣ�
��3�����жϳ���ֻ�е�M��EF��ʱ����P��D�غϣ�M��N�����غϣ���ʱt=4����M�ߵ�·��Ϊat�������⣬��at=8-$\frac{3}{2}$��at=8+$\frac{3}{2}$��
��� �⣺��1�����˶��У�AP=t��AD=4��
��PD=4-t��
�ߡ�ADG�ס�ACB��
��$\frac{AD}{AC}=\frac{DG}{BC}$��
��DG=3��
�ߡ�PDH��ADG��
��$\frac{DH}{DG}=\frac{PD}{AD}$��
��$\frac{DH}{3}=\frac{4-t}{4}$��
��DH=$\frac{3}{4}$��4-t��=3-$\frac{3}{4}$t��
��2����0��t��2ʱ����ͼ1��
S=S�ı���DEFG-S��GFH=3��2-$\frac{1}{2}$t��$\frac{3}{4}$t=6-$\frac{3}{8}$t2��
��2��t��4ʱ����ͼ2��
S=S�ı���DEFG=$\frac{1}{2}$��2[$\frac{3}{4}$��4-t��+$\frac{3}{4}$��6-t��]=$\frac{15}{2}$-$\frac{3}{2}$t��
��4��t��6ʱ����ͼ3��
S=S��GFH=$\frac{1}{2}$����6-t����$\frac{3}{4}$��6-t��=$\frac{3}{8}$t2-$\frac{9}{2}$t+$\frac{27}{2}$��
��6��t��8ʱ��S=0��
��3��������֪��ֻ�е�M��EF��ʱ����P��D�غϣ�M��N�����غϣ���ʱt=4��
��M�ߵ�·��Ϊat�������⣬��at=8-$\frac{3}{2}$��at=8+$\frac{3}{2}$��
��a=$\frac{13}{8}$��a=$\frac{19}{8}$��
���� �������ı����ۺ��⣬��Ҫ���������������ƣ������Σ��ı��ε�����ļ��㷽�����Ȿ��Ĺؼ��DZ�ʾ���߶Σ�Ҳ���ѵ㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ��������y=-x2+ax+b��x��������ҽ���A��B���㣬��y�������ύ�ڵ�C�����OCB=������OCA=�£���tan��-tan��=2��OC2=OA•OB��
��֪����ͼ��������y=-x2+ax+b��x��������ҽ���A��B���㣬��y�������ύ�ڵ�C�����OCB=������OCA=�£���tan��-tan��=2��OC2=OA•OB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
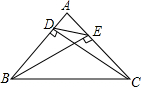 ��ͼ����ABC�У�DC��AB��D��BE��AC��E����˵��$\frac{DE}{BC}$=$\frac{AE}{AB}$��
��ͼ����ABC�У�DC��AB��D��BE��AC��E����˵��$\frac{DE}{BC}$=$\frac{AE}{AB}$���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com