

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源:不详 题型:解答题
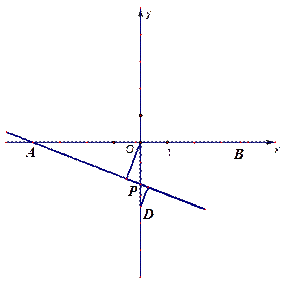
 的值(用含有k的式子表示.);
的值(用含有k的式子表示.); BOM =3S
BOM =3S DOM,且k为方程(k+7)(k+5)-(k+6)(k+5=
DOM,且k为方程(k+7)(k+5)-(k+6)(k+5= 的根,求直线BD的解析式.
的根,求直线BD的解析式. 值不变;②
值不变;② 值不变,请你判断其中哪一个结论是正确的,并说明理由并求出其值,
值不变,请你判断其中哪一个结论是正确的,并说明理由并求出其值,查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 )上一点,点P的横坐标为t,M是OP的中点(O是原点),以PM为对角线作正方形PDME.正方形PDME与△OAB公共部分的面积为S,求S与t之间的函数关系式,并求S的最大值.(图12-2、12-3供你探索问题时使用)
)上一点,点P的横坐标为t,M是OP的中点(O是原点),以PM为对角线作正方形PDME.正方形PDME与△OAB公共部分的面积为S,求S与t之间的函数关系式,并求S的最大值.(图12-2、12-3供你探索问题时使用)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| 1 |
| 3 |
| A.y1>y2 | B.y1=y2 | C.y1<y2 | D.无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com