
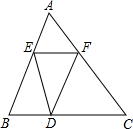
 (2012•大庆)如图所示,△ABC中,E、F、D分别是边AB、AC、BC上的点,且满足
(2012•大庆)如图所示,△ABC中,E、F、D分别是边AB、AC、BC上的点,且满足| AE |
| EB |
| AF |
| FC |
| 1 |
| 2 |
| AE |
| EB |
| AF |
| FC |
| 1 |
| 2 |
| AE |
| AB |
| AF |
| AC |
| 1 |
| 3 |
 ∵
∵| AE |
| EB |
| AF |
| FC |
| 1 |
| 2 |
| AE |
| AB |
| AF |
| AC |
| 1 |
| 3 |
| h |
| h′ |
| 1 |
| 3 |
| 1 |
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 (2012•大庆)如图所示,将一个圆盘四等分,并把四个区域分别标上I、Ⅱ、Ⅲ、Ⅳ,只有区域I为感应区域,中心角为60°的扇形AOB绕点0转动,在其半径OA上装有带指示灯的感应装置,当扇形AOB与区域I有重叠(原点除外)的部分时,指示灯会发光,否则不发光,当扇形AOB任意转动时,指示灯发光的概率为( )
(2012•大庆)如图所示,将一个圆盘四等分,并把四个区域分别标上I、Ⅱ、Ⅲ、Ⅳ,只有区域I为感应区域,中心角为60°的扇形AOB绕点0转动,在其半径OA上装有带指示灯的感应装置,当扇形AOB与区域I有重叠(原点除外)的部分时,指示灯会发光,否则不发光,当扇形AOB任意转动时,指示灯发光的概率为( )查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
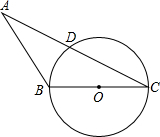 (2012•大庆)如图△ABC中,BC=3,以BC为直径的⊙O交AC于点D,若D是AC中点,∠ABC=120°.
(2012•大庆)如图△ABC中,BC=3,以BC为直径的⊙O交AC于点D,若D是AC中点,∠ABC=120°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com