
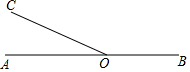
 在直线AB上任取一点O,过点O作射线OC、OD,使OC⊥OD,如果∠AOC=30°,OE平分∠BOD,求∠COE(要求:将图形补充完整,写出求解过程)
在直线AB上任取一点O,过点O作射线OC、OD,使OC⊥OD,如果∠AOC=30°,OE平分∠BOD,求∠COE(要求:将图形补充完整,写出求解过程) 分析 根据角的和差,可得∠BOD,根据角平分线的性质,可得∠DOE,根据角的和差,可得答案.
解答 解:如图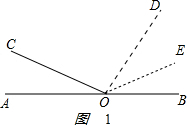 ,
,
由OC⊥OD,得
∠COD=90°.
由角的和差,得∠BOD=180°-∠AOC-∠COD=60°,
由OE平分∠BOD,得
∠DOE=$\frac{1}{2}$∠BOD=30°,
由角的和差,得
∠COE=∠COD+∠DOE=90°+30°=120°.
如图2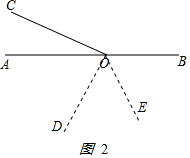 ,
,
由OC⊥OD,得
∠COD=90°.
由角的和差,得∠AOD=90°-∠AOC=60°,
∠BOD=180°-∠AOD=120°
由OE平分∠BOD,得
∠DOE=$\frac{1}{2}$∠BOD=60°,
由角的和差,得
∠COE=∠COD+∠DOE=90°+60°=150°.
综上所述:∠COE是150°或120°.
点评 本题考查了锤线,利用角的和差是解题关键,要分类讨论,以防遗漏.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
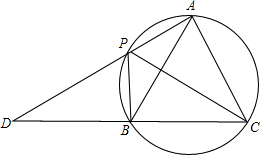 如图,四边形APBC是圆内接四边形,∠APB=120°,PC平分∠APB,AP,CB的延长线相交于点D.
如图,四边形APBC是圆内接四边形,∠APB=120°,PC平分∠APB,AP,CB的延长线相交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
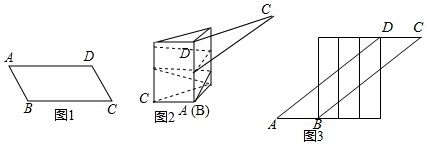
 如图,?ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,点E是BC的中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为4cm.
如图,?ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,点E是BC的中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为4cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com