
 如图,⊙O的半径为r.A,B为⊙O上的两个不同点;以B为圆心.BA为半径的圆交⊙O于另一点C.P为⊙O内一点,使得△PAB为正三角形,CP交⊙O于另一点Q.
如图,⊙O的半径为r.A,B为⊙O上的两个不同点;以B为圆心.BA为半径的圆交⊙O于另一点C.P为⊙O内一点,使得△PAB为正三角形,CP交⊙O于另一点Q.分析 (1)假设点P在⊙O上,求此时的正三角形的边长PB=$\sqrt{3}$r,但已知中“P为⊙O内一点”,所以AB=PB<$\sqrt{3}$r;
(2)本题介绍两种解法:
解法一:如图2,作辅助线,证明△POQ是等腰三角形即可得出结论.
解法二:如图3,作辅助线,证明△OQA是等边三角形,则OQ=QA,根据四点共圆中,圆外角等于内对角得:∠MAB=∠BCQ=∠BPC,根据平角的定义求得:∠QPA=∠QAP,所以QP=QA,由等量代换可以得出结论QP=OQ=r.
解答 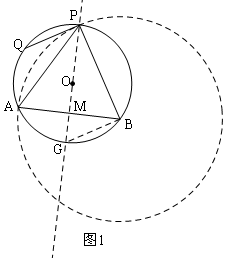 证明:(1)如图1,当P在圆O上时,过O作OG⊥AB于M,交⊙O于G,连接BG,
证明:(1)如图1,当P在圆O上时,过O作OG⊥AB于M,交⊙O于G,连接BG,
∴AM=BM,
∴GO是AB的中垂线,
∵△PAB是正三角形,
∴PA=PB=AB,∠PAB=60°,
∴P在GO上,
∴GP是⊙O的直径,
∴∠GBP=90°,
∵∠PGB=∠PAB=60°,
在Rt△PGB中,GP=2r,
sin60°=$\frac{PB}{GP}$=$\frac{\sqrt{3}}{2}$
$\frac{PB}{2r}$=$\frac{\sqrt{3}}{2}$,
PB=$\sqrt{3}$r,
∵P为⊙O内一点,
∴AB=PB<$\sqrt{3}$r;
(2)解法一:如图2,连接OQ、OA、OB、AC、BC,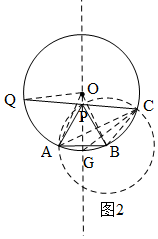
在⊙O中,∠PCA=$\frac{1}{2}$∠PBA=30°,
∵△PAB为等边三角形,
∴∠GPB=∠GPA=$\frac{1}{2}$∠APB=30°,
∵OA=OB,OG⊥AB,
∴∠AOG=$\frac{1}{2}$∠AOB,
在⊙O中,∠QOG=∠QOA+∠AOG,
=2∠QCA+∠AOG,
=60°+$\frac{1}{2}$∠AOB,
∵∠PCA=30°,∠GPB=30°,
∴∠QOG=∠PCA+∠GPB+∠ACB=∠GPB+∠PCB,
∵BP=BC,
∴∠BPC=∠BCP,
∴∠QOG=∠GPB+∠BPC=∠GPC=∠QPO,
∴PQ=OQ=r.
解法二:如图3,连接AC、OA、AQ、OQ、BC,延长QA交⊙B于M,
得:∠PCA=$\frac{1}{2}$∠PBA=30°,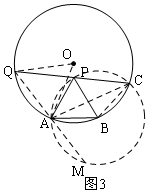
∠O=2∠PCA=2∠QCA=60°,
∴△OQA是等边三角形,
∴OQ=QA,
∵Q、A、B、C四点共圆,
∴∠MAB=∠BCQ=∠BPC,
∵∠QPA=180°-60°-∠BPC=120°-∠BPC,
∠QAP=180°-60°-∠MAB=120°-∠BPC,
∴∠QPA=∠QAP,
∴QP=QA,
∴QP=OQ=r.
点评 本题是圆的综合题,考查了圆周角定理、等边三角形的性质、等腰三角形的判定、特殊的三角函数的问题,第一问中确定动点A、B运动时,AB的长度的变化范围,第二问中确定PQ与中间量半径的关系是关键,从而使问题得以解决.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
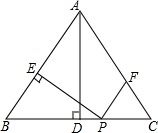 如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒,若以PE所在直线为对称轴,线段BD经轴对称变换后的图形为B′D′,当线段B′D′与线段AC有公共点时,则t的取值范围是$\frac{5}{6}$≤t≤$\frac{61}{60}$.
如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒,若以PE所在直线为对称轴,线段BD经轴对称变换后的图形为B′D′,当线段B′D′与线段AC有公共点时,则t的取值范围是$\frac{5}{6}$≤t≤$\frac{61}{60}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
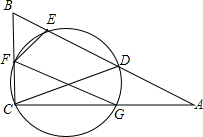 如图,D为Rt△ABC斜边AB上一点,以CD为直径的圆分别交△ABC三边于E、F、G三点,连接FE,FG.
如图,D为Rt△ABC斜边AB上一点,以CD为直径的圆分别交△ABC三边于E、F、G三点,连接FE,FG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
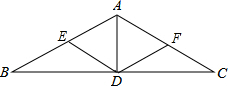 如图,在△ABC中,AB=AC,∠BAC=120°,AD是BC边的中线,点E、F分别是AB、AC的中点,连接DE、DF.
如图,在△ABC中,AB=AC,∠BAC=120°,AD是BC边的中线,点E、F分别是AB、AC的中点,连接DE、DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,求证:①BF=AC;②BF=2CE.
已知,如图△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,求证:①BF=AC;②BF=2CE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
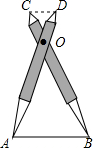 如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短,如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OD,OB=3OC),然后张开两脚,使A、B两个尖端分别在线段l的两个端点上,若CD=3.2cm,则AB的长为9.6cm.
如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短,如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OD,OB=3OC),然后张开两脚,使A、B两个尖端分别在线段l的两个端点上,若CD=3.2cm,则AB的长为9.6cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com