
����Ŀ��Ϊ�˸��ø��ƺ�����ˮ�ʣ����۹�˾��������10̨��ˮ�����豸������A��B�����ͺŵ��豸������ÿ̨�ļ۸��´�����ˮ�����±��������飺����һ̨A���豸�ȹ���һ̨B���豸��2��Ԫ������2̨A���豸�ȹ���3̨B���豸��6��Ԫ��
A�� | B�� | |
�۸���Ԫ/̨�� | a | b |
������ˮ������/�£� | 240 | 180 |
��1����a��b��ֵ��
��2�����۹�˾��Ԥ�㹺����ˮ�����豸���ʽ���105��Ԫ������Ϊ�ù�˾���ļ��ֹ�����
��3���ڣ�2���������£���ÿ��Ҫ������ˮ��������2040�֣�Ϊ�˽�Լ�ʽ�����Ϊ���۹�˾���һ����ʡǮ�Ĺ�����
���𰸡�(1) a��ֵΪ12��b��ֵΪ10��(2) ���й���Ϊ����A�ͺ�Ϊ0��B�ͺ�Ϊ10̨����A�ͺ�Ϊ1̨��B�ͺ�Ϊ9̨����A�ͺ�Ϊ2̨��B�ͺ�Ϊ8̨����3�ֹ�����(3) ��˾��ʡǮ��һ�ֹ���Ϊ������A�ʹ�����1̨��B�ʹ�����9̨��
�������������������1������A�͵ļ۸���a��Ԫ������B�͵��豸b��Ԫ�����ݹ���һ̨A�ͺ��豸�ȹ���һ̨B�ͺ��豸��2��Ԫ������2̨A���豸�ȹ���3̨B�ͺ��豸��6��Ԫ�����з�������⣮
��2���蹺��A�ͺ��豸m̨����B��Ϊ��10-m��̨������ʹ���۹�˾������ˮ�����豸���ʽ���105��Ԫ�������ó�����ʽ��
��3�����ã�2���������������ó��𰸣�
�����������1������A�͵ļ۸���a��Ԫ������B�͵��豸b��Ԫ��
![]() ��
��
��ã� ![]() ��
��
��a��ֵΪ12��b��ֵΪ10��
��2���蹺��A�ͺ��豸m̨��
12m+10��10��m����105��
��ã�m��![]() ��
��
�����й���Ϊ����A�ͺ�Ϊ0��B�ͺ�Ϊ10̨��
��A�ͺ�Ϊ1̨��B�ͺ�Ϊ9̨��
��A�ͺ�Ϊ2̨��B�ͺ�Ϊ8̨����3�ֹ�����
��3����x=0��10��x=10ʱ��ÿ�µ���ˮ������Ϊ��200��10=2000����2040�֣����������⣬Ӧ��ȥ��
��x=1��10��x=9ʱ��ÿ�µ���ˮ������Ϊ��240+200��9=2040��=2040�֣�����������
��ʱ���豸�����ʽ�Ϊ��12+10��9=102��Ԫ��
��x=2��10��x=8ʱ��ÿ�µ���ˮ������Ϊ��240��2+200��8=2080����2040�֣�����������
��ʱ���豸�����ʽ�Ϊ��12��2+10��8=104��Ԫ��
���ԣ�Ϊ�˽�Լ�ʽ𣬸ù�˾��ʡǮ��һ�ֹ���Ϊ������A�ʹ�����1̨��B�ʹ�����9̨��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�ǵ��������Σ����ϵĸ�Ϊ8cm�����Ϊ40cm2����������ε��ܳ���_______cm.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�ĶԽ��߽��ڵ�E����AE=EC��BE=ED����ABΪֱ���İ�Բ����E��Բ��ΪO��
��1������ͼ1����֤���ı���ABCD�����Σ� 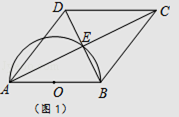
��2����ͼ2����CD���ӳ������Բ�����ڵ�F����ֱ֪��AB=8�� ������OE�����OBE�������
��������AOE�������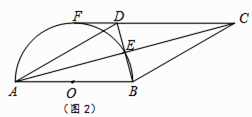
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֵ��֤��
��![]() ��0��1��2��5����ʱ���������ʽ
��0��1��2��5����ʱ���������ʽ![]() ��ֵ���ֱ�õ�5��2��1��2��17��������x��ȡֵ�����仯ʱ������ʽ
��ֵ���ֱ�õ�5��2��1��2��17��������x��ȡֵ�����仯ʱ������ʽ![]() ��ֵȴ��һ��ȷ���ķ�Χ��ͨ�������֤���Է�������ֵ�ܴ��ڻ����1������1����������Сֵ��
��ֵȴ��һ��ȷ���ķ�Χ��ͨ�������֤���Է�������ֵ�ܴ��ڻ����1������1����������Сֵ��
��ʽ��֤��
���ǿ�����ѧ����֪ʶ����![]() ���к�ȱ��Σ�
���к�ȱ��Σ�![]() ����ע�����ֱ��η����ɳ�Ϊ���䷽����
����ע�����ֱ��η����ɳ�Ϊ���䷽���� ![]() ��
��![]() ����������xȡ��ֵ������ʽ
����������xȡ��ֵ������ʽ![]() ��ֵ��С��1������СֵΪ1��
��ֵ��С��1������СֵΪ1��
Ǩ��ʵ֤��
��1�����������䷽���ķ�����ȷ��![]() ����СֵΪ3��
����СֵΪ3��
��2����![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1������ʵ������ABC�У���A=90������B=22.5�㣬�뻭��һ��ֱ�߰ѡ�ABC�ָ���������������Σ�������ָ���������������εǵĶ�������Ҫ�������ֲ�ͬ�ķָ����
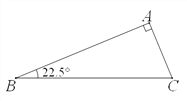
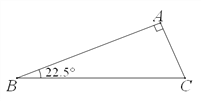
��2������̽������ABC�У���С�ڽǡ�B=24�㣬����ABC��һֱ�߷ָ���������������Σ��뻭����Ӧʾ��ͼ��д����ABC����ڽǵ����п���ֵ��
��3�����뷢�֣���һ���������ܱ�һֱ�߷ָ���������������Σ�������ʲô����������������д����������������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾��![]() ���ֿ�ֱ��л���16̨��12̨����Ҫ�����ס������أ����м���Ҫ15̨���ҵ���Ҫ13̨����֪
���ֿ�ֱ��л���16̨��12̨����Ҫ�����ס������أ����м���Ҫ15̨���ҵ���Ҫ13̨����֪![]() ���زֿ������ף������ػ����ķ���������������ʾ��
���زֿ������ף������ػ����ķ���������������ʾ��
![]() ���A�ֿ��x̨����ȥ�أ����ú�x�Ĵ���ʽ��ȫ������ұ���
���A�ֿ��x̨����ȥ�أ����ú�x�Ĵ���ʽ��ȫ������ұ���
�������˷��ñ��������˷�����
������ Ŀ�ĵ��˷� | A | B | ������ Ŀ�ĵ����� | A | B | �ϼ� | |
�� | 500 | 300 | �� | x | 15 | ||
�� | 400 | 600 | �ҵ� | 13 | |||
�ϼ� | 16 | 12 | 28 |
![]() �����˷�ΪyԪ����y��x֮��ĺ�������ʽ����д���Ա���x��ȡֵ��Χ��
�����˷�ΪyԪ����y��x֮��ĺ�������ʽ����д���Ա���x��ȡֵ��Χ��
![]() �ɻ������˷�������֪����n�ֵ��˷�������n��ֵ��
�ɻ������˷�������֪����n�ֵ��˷�������n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y=3x2����ƽ��3����λ��������ƽ��2����λ����ô�õ��������ߵĽ���ʽΪ��������
A.y=3 ![]() +3
+3
B.y=3 ![]() +3
+3
C.y=3 ![]() -3
-3
D.y=3 ![]() -3
-3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ǿ��Сѧ����ȫ�ͽ���������ijУ��֯�ˡ�����ˮ����ͨ��ȫ��������֪ʶ������Ϊ�����ھ����б�������İ༶��ѧУ����������Ʒ�̳�һ���Թ������ɸ����������ÿ������ļ۸���ͬ��ÿ������ļ۸���ͬ��������1�������1��������159Ԫ�����������۵�2����9Ԫ��
��1�������������ĵ��۸��Ƕ���Ԫ��
��2������ѧУʵ���������һ���Թ������������20������Ҫ���������������ܷ��ò�����1550Ԫ��ѧУ�����Թ�����ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ƕ��κ��� y=ax2+bx+c��a��0����ͼ���һ���֣������������⣺��a+b+c=0����b��2a����ax2+bx+c=0�������ֱ�Ϊ-3��1����a-2b+c��0��������ȷ�������� �� ��ֻҪ����д��ȷ�������ţ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com