
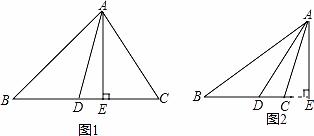
在△ABC中,AD是角平分线,AE是高线
① 如图①所示,∠ABC=40°,∠ACB=70°,求∠DAE。
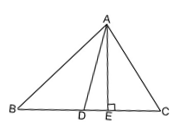
② 如图②所示,∠ABC=30°,∠ACB=110°,求∠DAE。
 ③ 根据①、②两题的计算结果,请猜想∠DAE与∠ABC和∠ACB之间的关系(用等式表示出来)
③ 根据①、②两题的计算结果,请猜想∠DAE与∠ABC和∠ACB之间的关系(用等式表示出来)
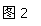

解:①∵∠ABC=40°,∠ACB=70°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=70°,
∵AD平分∠BAC,
∴∠CAD= ∠BAC=
∠BAC= ×70°=35°,
×70°=35°,
∵AE⊥BC,
∴∠AEC=90°,
∵∠C=70°,
∴∠EAC=180°﹣90°﹣70°=20°,
∴∠DAE=∠DAC﹣∠EAC=35°﹣20°=15°.
②∵∠ABC=30°,∠ACB=110°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=40°,
∵AD平分∠BAC,
∴∠CAD= ∠BAC=
∠BAC= ×40°=20°,
×40°=20°,
∵AE⊥BC,
∴∠AEC=90°,
∵∠C=110°,
∴∠EAC=∠ACB﹣∠AEC=110°﹣90°=20°,
∴∠DAE=∠DAC+∠EAC=20°+20°=40°.
③∠DAE= ∠ACB﹣
∠ACB﹣ ∠ABC,理由如下:
∠ABC,理由如下:
分为两种情况:如图1,
∠BAC=180°﹣(∠ABC+∠ACB),
∵AD平分∠BAC,
∴∠DAC= [180°﹣(∠ABC+∠ACB)]=90°﹣
[180°﹣(∠ABC+∠ACB)]=90°﹣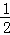 ∠ABC﹣
∠ABC﹣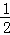 ∠ACB,
∠ACB,
∵AE⊥BC,
∴∠AEC=90°,
∴∠CAE=90°﹣∠ACB,
∴∠DAE=∠DAC﹣∠EAC=(90°﹣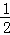 ∠ABC﹣
∠ABC﹣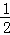 ∠ACB)﹣(90°﹣∠ACB)=
∠ACB)﹣(90°﹣∠ACB)=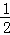 ∠ACB﹣
∠ACB﹣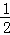 ∠ABC;
∠ABC;
如图2,
∠BAC=180°﹣∠ABC﹣∠ACB,
∵AD平分∠BAC,
∴∠CAD=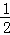 ∠BAC=
∠BAC=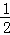 ×(180°﹣∠ABC﹣∠ACB)=90°﹣
×(180°﹣∠ABC﹣∠ACB)=90°﹣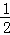 ∠ABC﹣
∠ABC﹣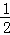 ∠ACB,
∠ACB,
∵AE⊥BC,
∴∠AEC=90°,
∴∠EAC=∠ACB﹣∠AEC=∠ACB﹣90°,
∴∠DAE=∠DAC+∠CAD=90°﹣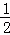 ∠ABC﹣
∠ABC﹣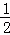 ∠ACB+∠ACB﹣90°=
∠ACB+∠ACB﹣90°=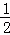 ∠ACB﹣
∠ACB﹣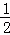 ∠ABC.
∠ABC.


科目:初中数学 来源:2014-2015学年江苏省东台市九年级上学期第二次月考数学试卷(解析版) 题型:解答题
(本题满分10分)有一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m.
⑴ 在如图所示的直角坐标系中,求出该抛物线的解析式;
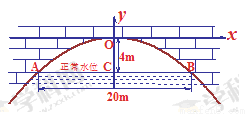
⑵ 设正常水位时桥下的水深为2m,为保证过往船只顺利航行,桥下水面的宽度不得小于18m,求水深超过多少米时就会影响过往船只在桥下的顺利航行.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省娄底市九年级上学期期末模拟考试数学试卷(解析版) 题型:选择题
在相同时刻的物高与影长成比例,如果高为1.5m的测杆的影长为2.5m,那么影长为30m的旗杆的高是( )
A.20m B.16m C.18m D.15m
查看答案和解析>>
科目:初中数学 来源: 题型:
王老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车发生故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,如果准时到校.在课堂上,李老师请学生画出他行进的路程y(千米)与行进时间t(小时)的函数图象的示意图,同学们画出的图象如图所示,你认为正确的是( )

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.请找出图2中的全等三角形,并给予证明(不再添加其它线段,不再标注或使用其它字母).
解:(1)你找到的全等三角形是: ;
(2)证明:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com