
| A. | 1-$\sqrt{2}$ | B. | -1 | C. | 1±$\sqrt{2}$ | D. | 1$±\sqrt{2}$或-1 |
分析 根据题中的新定义,分x<-x与x>-x两种情况求出所求方程的解即可.
解答 解:当x<-x,即x<0时,方程化为x=$\frac{2x+1}{x}$,
去分母得:x2-2x-1=0,
解得:x=$\frac{2±2\sqrt{2}}{2}$=1±$\sqrt{2}$,
即x1=1+$\sqrt{2}$(舍去),x2=1-$\sqrt{2}$,
当x>-x,即x>0时,方程化为-x=$\frac{2x+1}{x}$,
去分母得:x2+2x+1=0,即(x+1)2=0,
解得:x1=x2=-1(舍去),
经检验x=1-$\sqrt{2}$是分式方程的解,
综上,所求方程的解为1-$\sqrt{2}$,
故选A.
点评 此题考查了分式方程的解,弄清题中的新定义是解本题的关键.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:解答题
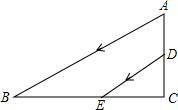 如图,AB、DE是一束平行的阳关从教室的窗口AD射入的平面示意图,且阳光AB与地面BC的夹角为30°,阳光在室内地面的影长BE=2$\sqrt{3}$m,窗口的下檐到教室地面的距离DC=1.2m.求窗顶到地面的距离AC的长.
如图,AB、DE是一束平行的阳关从教室的窗口AD射入的平面示意图,且阳光AB与地面BC的夹角为30°,阳光在室内地面的影长BE=2$\sqrt{3}$m,窗口的下檐到教室地面的距离DC=1.2m.求窗顶到地面的距离AC的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据计算CD的长为22cm(精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据计算CD的长为22cm(精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
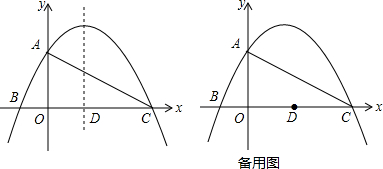
 如图,在三角形ABC中,B(2,0),把三角形ABC沿AC边平移,使A点到C点,三角形ABC变换为三角形CED,已知C(0,3.5),请写出A,D,E的坐标,并说出平移的过程.
如图,在三角形ABC中,B(2,0),把三角形ABC沿AC边平移,使A点到C点,三角形ABC变换为三角形CED,已知C(0,3.5),请写出A,D,E的坐标,并说出平移的过程.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1+$\sqrt{2}$或-1 | B. | 2-$\sqrt{2}$ | C. | 1+$\sqrt{2}$或1-$\sqrt{2}$ | D. | 1-$\sqrt{2}$或-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
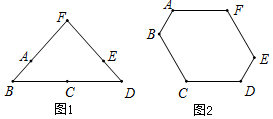 由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)
由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com