
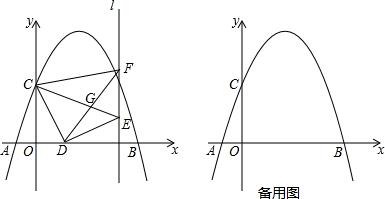
���� ��1����A���B���������y=ax2+bx+3�еõ�����a��b�ķ����飬Ȼ��ⷽ�������a��b���ɵõ������߽���ʽ��
��2����ͼ1�������C�����꣬�ٸ�����ת�����ʵõ�CD=DE����CDE=90�㣬��֤����OCD�ա�HDE�õ�HD=OC=3������˵���ı���OCFHΪ���εõ�HF=OC=3��Ȼ�����ù��ɶ�������DF��
��3�������á�CDE�͡�DFH���ǵ���ֱ�������εõ���DCE=45�㣬��DFH=45�㣬�����С�DFC=45�㣬���֤����DCG�ס�DFC���������Ƶ����ʵ�$\frac{CD}{DF}$=$\frac{DG}{DC}$����DGC=��DCF�������������Ʊȿɼ����CD=$\sqrt{10}$�����á�DCF=��2�õ���CGD=��2��Ȼ����Rt��OCD�������2������ֵ���ɵõ�tan��CGD��ֵ��
�ڸ��ݡ�DCG�ס�DFC�õ�HD=OC=3��EH=OD=1����E��4��1����ȡCE���е�M����ͼ2�������߶ε��е����깫ʽ�õ�M��2��2�������ݵ���ֱ�������ε������ж�DP����CE���е�M�����������ô���ϵ�������ֱ��DP�Ľ���ʽΪy=2x-2��Ȼ��ⷽ����$\left\{\begin{array}{l}{y=-\frac{3}{5}{x}^{2}+\frac{12}{5}x+3}\\{y=2x-2}\end{array}\right.$�ɵ�P�����꣮
��� �⣺��1����������y=ax2+bx+3��x����A��-1��0����B��5��0����
��$\left\{\begin{array}{l}{a-b+3=0}\\{25a+5b+3=0}\end{array}\right.$�����$\left\{\begin{array}{l}{a=-\frac{3}{5}}\\{b=\frac{12}{5}}\end{array}\right.$��
�������߽���ʽΪ��y=-$\frac{3}{5}$x2+$\frac{12}{5}$x+3��
��2����x=0ʱ��y=-$\frac{3}{5}$x2+$\frac{12}{5}$x+3=3����C��0��3������ͼ1��
��CD�Ƶ�D˳ʱ����ת90��õ��߶�DE��
��CD=DE����CDE=90�㣬
�ߡ�2+��3=90�㣬
����1+��2=90�㣬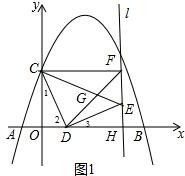
���1=��3��
�ڡ�OCD�͡�HDE��
$\left\{\begin{array}{l}{��DOC=��EHD}\\{��1=��3}\\{CD=DE}\end{array}\right.$��
���OCD�ա�HDE��
��HD=OC=3��
��CF��BF��
���ı���OCFHΪ���Σ�
��HF=OC=3��
��DF=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$��
��3���١ߡ�CDE�͡�DFH���ǵ���ֱ�������Σ���ͼ1��
���DCE=45�㣬��DFH=45�㣬
���DFC=45�㣬
����CDG=��FDC��
���DCG�ס�DFC��
��$\frac{CD}{DF}$=$\frac{DG}{DC}$����DGC=��DCF��
��$\frac{CD}{3\sqrt{2}}$=$\frac{\frac{5\sqrt{2}}{3}}{CD}$�����CD=$\sqrt{10}$��
��CF��OH��
���DCF=��2��
���CGD=��2��
��Rt��OCD��OD=$\sqrt{C{D}^{2}-O{C}^{2}}$=$\sqrt{��\sqrt{10}��^{2}-{3}^{2}}$=1��
��tan��2=$\frac{OC}{OD}$=3��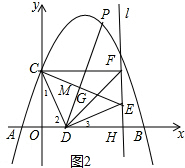
��tan��CGD=3��
�ڡ�OD=1��
��D��1��0����
�ߡ�OCD�ա�HDE��
��HD=OC=3��EH=OD=1��
��E��4��1����
ȡCE���е�M����ͼ2����M��2��2����
�ߡ�DCEΪ����ֱ�������Σ���EDP=45�㣬
��DP����CE���е�M��
��ֱ��DP�Ľ���ʽΪy=mx+n��
��D��1��0����M��2��2�������$\left\{\begin{array}{l}{m+n=0}\\{2m+n=2}\end{array}\right.$�����$\left\{\begin{array}{l}{m=2}\\{n=-2}\end{array}\right.$��
��ֱ��DP�Ľ���ʽΪy=2x-2��
�ⷽ����$\left\{\begin{array}{l}{y=-\frac{3}{5}{x}^{2}+\frac{12}{5}x+3}\\{y=2x-2}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{1+2\sqrt{19}}{3}}\\{y=\frac{4\sqrt{19}-4}{3}}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{1-2\sqrt{19}}{3}}\\{y=\frac{-4\sqrt{19}-4}{3}}\end{array}\right.$����ȥ����
��P��������$\frac{1+2\sqrt{19}}{3}$��$\frac{4\sqrt{19}-4}{3}$����
���� ���⿼���˶��κ������ۺ��⣺�������յ���ֱ�������ε����ʺ���ת�����ʣ������ô���ϵ������һ�κ����Ͷ��κ�������ʽ����ͨ���ⷽ��������������ֱ�ߵĽ������ꣻ������������ȫ�ȵ�֪ʶ֤���߶���ȣ��������Ʊ����߶εij���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
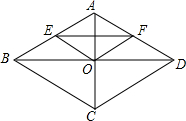 ��ͼ������ֽƬABCD�ĶԽ���AC��BD�ཻ�ڵ�O���۵�ֽƬʹ��A���O�غϣ��ۺ�ΪEF����AB=5��BD=8�����OEF�����Ϊ��������
��ͼ������ֽƬABCD�ĶԽ���AC��BD�ཻ�ڵ�O���۵�ֽƬʹ��A���O�غϣ��ۺ�ΪEF����AB=5��BD=8�����OEF�����Ϊ��������| A�� | 12 | B�� | 6 | C�� | 3 | D�� | $\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��A=��D | B�� | AB=AD | C�� | AC��BD | D�� | CAƽ�֡�BCD |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
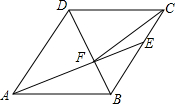 ��ͼ��������ABCD�У�AB=6����DAB=60�㣬AE�ֱ�BC��BD�ڵ�E��F��CE=2������CF�����½��ۣ��١�ABF�ա�CBF���ڵ�E��AB�ľ�����2$\sqrt{3}$����tan��DCF=$\frac{3\sqrt{3}}{7}$���ܡ�ABF�����Ϊ12$\sqrt{3}$������һ���������Ǣ٢ڢۣ���������ȷ���۵���Ŷ����ں����ϣ��٢ڢۣ�
��ͼ��������ABCD�У�AB=6����DAB=60�㣬AE�ֱ�BC��BD�ڵ�E��F��CE=2������CF�����½��ۣ��١�ABF�ա�CBF���ڵ�E��AB�ľ�����2$\sqrt{3}$����tan��DCF=$\frac{3\sqrt{3}}{7}$���ܡ�ABF�����Ϊ12$\sqrt{3}$������һ���������Ǣ٢ڢۣ���������ȷ���۵���Ŷ����ں����ϣ��٢ڢۣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
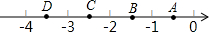 ��ͼ����������A��B��C��D�ĸ����У����ʾ4-$\sqrt{28}$�ĵ���ӽ����ǣ�������
��ͼ����������A��B��C��D�ĸ����У����ʾ4-$\sqrt{28}$�ĵ���ӽ����ǣ�������| A�� | ��A | B�� | ��B | C�� | ��C | D�� | ��D |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com