
【题目】如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③CP=CQ;④BO=OE;⑤∠AOB=60°,恒成立的结论有

A. ①③⑤ B. ①③④⑤ C. ①②③⑤ D. ①②③④⑤
【答案】C
【解析】
①根据全等三角形的判定方法,证出△ACD≌△BCE,即可得出AD=BE.
③先证明△ACP≌△BCQ,即可判断出CP=CQ,③正确;
②根据∠PCQ=60°,可得△PCQ为等边三角形,证出∠PQC=∠DCE=60°,得出PQ∥AE,②正确.
④没有条件证出BO=OE,得出④错误;
⑤∠AOB=∠DAE+∠AEO=∠DAE+∠ADC=∠DCE=60°,⑤正确;即可得出结论.
∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60,
∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
在△ACD和△BCE中,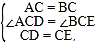
∴△ACD≌△BCE(SAS),
∴AD=BE,结论①正确,
∵△ACD≌△BCE,
∴∠CAD=∠CBE,
又∵![]()
∴![]()
∴![]()
在△ACP和△BCQ中,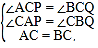
∴△ACP≌△BCQ(AAS),
∴CP=CQ,结论③正确;
又∵![]()
∴△PCQ为等边三角形,
∴![]()
∴PQ∥AE,结论②正确,
∵△ACD≌△BCE,
∴∠ADC=∠AEO,
∴![]()
∴结论⑤正确.没有条件证出BO=OE,④错误;
综上,可得正确的结论有4个:①②③⑤.
故选:C.


科目:初中数学 来源: 题型:
【题目】本学期学习了一元一次方程的解法,下面是林林同学的解题过程:解方程![]() =1
=1
解:方程两边同时乘以6,得:![]() ×6=1×6…………第①步
×6=1×6…………第①步
去分母,得:2(2x+1)-x+2=6………………第②步
去括号,得:4x+2-x+2=6…………………第③步
移项,得:4x-x=6-2-2…………………第④步
合并同类项,得:3x=2…………………………第⑤步
系数化1,得:x=![]() …………………………第⑥步
…………………………第⑥步
上述林林的解题过程从第______步开始出现错误,错误的原因是______.
请你帮林林改正错误,写出完整的解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有除颜色外其余均相同的5个小球,其中红球3个(记为A1 , A2 , A3),黑球2个(记为B1 , B2).
(1)若先从袋中取出m(m>0)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,填空:①若A为必然事件,则m的值为
②若A为随机事件,则m的取值为
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,用树状图或列表法求这个事件的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)平面内将一副三角板按如图1所示摆放,∠EBC= °;
(2)平面内将一副三角板按如图2所示摆放,若∠EBC=165°,那么∠α= °;
(3)平面内将一副三角板按如图3所示摆放,∠EBC=115°,求∠α的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AC为⊙O的直径,PA为⊙O的切线,切点为A,B为⊙O上一点,且BC∥PO.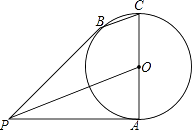
(1)求证:PB为⊙O的切线;
(2)若⊙O的半径为1,PA=3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
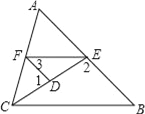
【题目】如图,已知∠1,∠2互为补角,且∠3=∠B,
(1)求证:∠AFE=∠ACB
(2)若CE平分∠ACB,且∠1=80°,∠3=45°,求∠AFE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国明代著名数学家程大位的《算法统宗》一书中记载了一些诗歌形式的算题,其中有一个“百羊问题”:甲赶群羊逐草茂,乙拽肥羊一只随其后;戏问甲及一百否?甲云所说无差谬,若得这般一群凑,再添半群小半群,得你一只来方凑.玄机奥妙谁猜透.题目的意思是:甲赶了一群羊在草地上往前走,乙牵了一只肥羊紧跟在甲的后面.乙问甲:“你这群羊有一百只吗?”甲说:“如果再有这么一群,再加半群,又加四分之一群,再把你的一只凑进来,才满100只.”请问甲原来赶的羊一共有多少只?如果设甲原来赶的羊一共有![]() 只,那么可列方程为______________.
只,那么可列方程为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程
如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:

∵DE∥BC(已知)
∴∠ADE= .( )
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF=![]() ,
,
∠ABE=![]() .( )
.( )
∴∠ADF=∠ABE
∴DF∥ .( )
∴∠FDE=∠DEB. ( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com