
【题目】如图,已知抛物线经过点![]() ,
,![]() ,
,![]() 三点.
三点.

![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 若点
若点![]() 是线段
是线段![]() 上的点(不与
上的点(不与![]() ,
,![]() 重合),过
重合),过![]() 作
作![]() 轴交抛物线于
轴交抛物线于![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
![]() 在
在![]() 的条件下,连接
的条件下,连接![]() ,
,![]() ,是否存在点
,是否存在点![]() ,使
,使![]() 的面积最大?若存在,求
的面积最大?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在;当
;(3)存在;当![]() 时,
时,![]() 的面积最大,最大值为
的面积最大,最大值为![]() .
.
【解析】
(1)已知了抛物线上的三个点的坐标,直接利用待定系数法即可求出抛物线的解析式.
(2)先利用待定系数法求出直线BC的解析式,已知点M的横坐标,代入直线BC、抛物线的解析式中,可得到M、N点的坐标,N、M纵坐标的差的绝对值即为MN的长.
(3)设MN交x轴于D,那么△BNC的面积可表示为:S△BNC=S△MNC+S△MNB=![]() MN(OD+DB)=
MN(OD+DB)=![]() MNOB,MN的表达式在(2)中已求得,OB的长易知,由此列出关于S△BNC、m的函数关系式,根据函数的性质即可判断出△BNC是否具有最大值.
MNOB,MN的表达式在(2)中已求得,OB的长易知,由此列出关于S△BNC、m的函数关系式,根据函数的性质即可判断出△BNC是否具有最大值.
![]() 设抛物线的解析式为:
设抛物线的解析式为:![]() ,则:
,则:
![]() ,
,![]() ;
;
∴抛物线的解析式:![]() .
.
![]() 设直线
设直线![]() 的解析式为:
的解析式为:![]() ,则有:
,则有:
![]() ,
,
解得![]() ;
;
故直线![]() 的解析式:
的解析式:![]() .
.
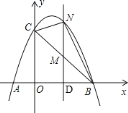
已知点![]() 的横坐标为
的横坐标为![]() ,
,![]() ,则
,则![]() 、
、![]() ;
;
∴故![]() .
.
![]() 如图;
如图;
∵![]() ,
,
∴![]() ;
;
∴当![]() 时,
时,![]() 的面积最大,最大值为
的面积最大,最大值为![]() .
.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】(1)请画出△ABC关于直线m(直线m上各点的横坐标都为1)对称的图形.(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′、B′、C′三点的坐标.
(3)平面内任一点P(x,y)关于直线m对称点的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系,下列说法:①乙晚出发1小时;②乙出发3小时后追上甲;③甲的速度是4千米/时;④乙先到达B地.其中正确的是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长一定的正方形ABCD,Q是CD上一动点,AQ交BD于点M,过M作MN⊥AQ交BC于N点,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;
②MP=![]() BD;③BN+DQ=NQ;④
BD;③BN+DQ=NQ;④![]() 为定值。其中一定成立的是_______.
为定值。其中一定成立的是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
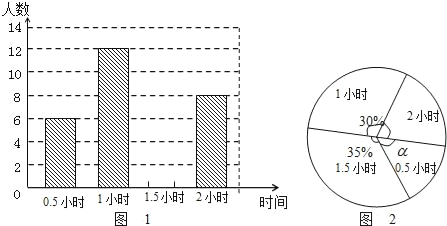
【题目】为了贯彻“减负增效”精神,掌握九年级600名学生每天的自主学习情况,某校学生会随机抽查了九年级的部分学生,并调查他们每天自主学习的时间.根据调查结果,制作了两幅不完整的统计图(图1,图2),请根据统计图中的信息回答下列问题:
(1)本次调查的学生人数是 人;
(2)图2中α是 度,并将图1条形统计图补充完整;
(3)请估算该校九年级学生自主学习时间不少于1.5小时有 人;
(4)老师想从学习效果较好的4位同学(分别记为A、B、C、D,其中A为小亮)随机选择两位进行学习经验交流,用列表法或树状图的方法求出选中小亮A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图(不要求写出作法,请保留作图痕迹):

(1)如图1,经过已知直线![]() 外一点
外一点![]() 作这条直线的垂线;
作这条直线的垂线;
(2)如图2,已知等腰三角形底边长为![]() ,底边上的高为
,底边上的高为![]() ,求作这个等腰三角形.
,求作这个等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜加工公司先后两次收购某时令蔬菜200吨,第一批蔬菜价格为2000元/吨,因蔬菜大量上市,第二批收购时价格变为500元/吨,这两批蔬菜共用去16万元.
(1)求两批次购蔬菜各购进多少吨?
(2)公司收购后对蔬菜进行加工,分为粗加工和精加工两种:粗加工每吨利润400元,精加工每吨利润800元.要求精加工数量不多于粗加工数量的三倍.为获得最大利润,精加工数量应为多少吨?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com