
【题目】如图,AB是半圆O的直径,C.E在半圆O上,CD⊥AB于点D,且CD=![]() .
.
(1)如图1.若点C是![]() 的中点,求AE的长;
的中点,求AE的长;
(2)如图2,若∠B=30°,连接CE,点P为CE中点,连接DP,交AE于点F,记以C为圆心,CP为半径的圆为⊙C.探究AE与⊙C的位置关系,并说明理由.
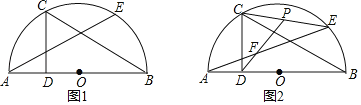
【答案】(1)AE=2![]() ;(2)AE与⊙C相切,理由见解析.
;(2)AE与⊙C相切,理由见解析.
【解析】
(1)连接OC,交AE于点F,由点C是![]() 的中点,根据垂径定理可得,得OC⊥AE,
的中点,根据垂径定理可得,得OC⊥AE,![]() ,依据AAS证明△AFO≌△CDO,即可求得AE的长;
,依据AAS证明△AFO≌△CDO,即可求得AE的长;
(2)根据点P为CE中点,得CP=![]() CE,由同弧所对圆周角相等得∠E=∠B=30°,作CG⊥AE于G,依据含有30度的直角三角形的性质得到CG=
CE,由同弧所对圆周角相等得∠E=∠B=30°,作CG⊥AE于G,依据含有30度的直角三角形的性质得到CG=![]() CE,从而CP=CG,即可证明AE与⊙C相切.
CE,从而CP=CG,即可证明AE与⊙C相切.
解:(1)如图1,
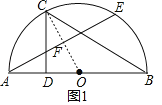
连接OC,交AE于点F,
![]() 点C是
点C是![]() 的中点,
的中点,![]() ,2
,2![]() ,
,![]() ,
,![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
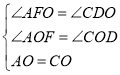
![]() ≌
≌![]() ,
,![]() ,
,![]() ;
;
(2)AE与⊙C相切,理由如下:
如图2,作CG⊥AE于G,则![]() ,
,
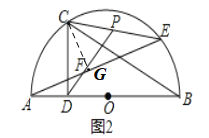
∵点P为CE中点,
![]() ,
,
∵![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴CG=CP,
∴以C为圆心,CP为半径的圆为⊙C与AE相切.
所以AE与⊙C相切.


科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象都经过点A(m,2).
)的图象都经过点A(m,2).

(1)求点A的坐标及反比例函数的表达式;
(2)设一次函数![]() 的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.
的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代数学专著,在数学上有其独到的成就,不仅最早提到了分数问题,也首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱.问买鸡的人数、鸡的价格各是多少?请解答上述问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
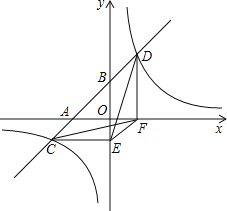
【题目】如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数y=![]() 的图象相交于C、D两点,分别过C、D两点作y轴和x轴的垂线,垂足分别为E、F,连接CF、DE.下列四个结论:①△CEF与△DEF的面积相等;②△AOB∽△FOE;③AC=BD;④tan∠BAO=a;其中正确的结论是_____.(把你认为正确结论的序号都填上)
的图象相交于C、D两点,分别过C、D两点作y轴和x轴的垂线,垂足分别为E、F,连接CF、DE.下列四个结论:①△CEF与△DEF的面积相等;②△AOB∽△FOE;③AC=BD;④tan∠BAO=a;其中正确的结论是_____.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )
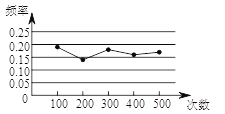
A. 袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球
B. 掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6
C. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
D. 掷一枚质地均匀的硬币,落地时结果是“正面向上”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某隧道洞的内部截面顶部是抛物线形,现测得地面宽 AB=10m,隧道顶点O到地面AB的距离为5m,
(1)建立适当的平面直角坐标系,幵求该抛物线的解析式;
(2)一辆小轿车长 4.5米,宽2米,高1.5米,同样大小的小轿车通过该隧道,最多能有 几辆车幵行?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:
①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.
其中正确的有( )
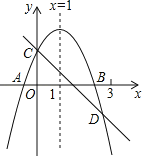
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两支仪仗队队员的身高(单位:厘米)如下:
甲队:178,177,179,178,177,178,177,179,178,179;
乙队:178,179,176,178,180,178,176,178,177,180;
(1)甲队队员身高的平均数为 厘米,乙队队员身高的平均数为 厘米;
(2)你认为哪支仪仗队更为整齐?简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( ).
A. “打开电视机,正在播放《动物世界》”是必然事件
B. 某种彩票的中奖概率为![]() ,说明每买1000张,一定有一张中奖
,说明每买1000张,一定有一张中奖
C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为![]()
D. 想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com