
【题目】如图,△ABC为等边三角形,AB=2.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为 . 
【答案】![]()
【解析】解:∵△ABC是等边三角形, ∴∠ABC=∠BAC=60°,AC=AB=2,
∵∠PAB=∠ACP,
∴∠PAC+∠ACP=60°,
∴∠APC=120°,
当PB⊥AC时,PB长度最小,设垂足为D,如图所示: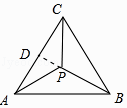
此时PA=PC,
则AD=CD= ![]() AC=1,∠PAC=∠ACP=30°,∠ABD=
AC=1,∠PAC=∠ACP=30°,∠ABD= ![]() ∠ABC=30°,
∠ABC=30°,
∴PD=ADtan30°= ![]() AD=
AD= ![]() ,BD=
,BD= ![]() AD=
AD= ![]() ,
,
∴PB=BD﹣PD= ![]() ﹣
﹣ ![]() =
= ![]() ;
;
所以答案是: ![]() .
.
【考点精析】根据题目的已知条件,利用等边三角形的性质和圆周角定理的相关知识可以得到问题的答案,需要掌握等边三角形的三个角都相等并且每个角都是60°;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( ) 
A.△AEE′是等腰直角三角形
B.AF垂直平分EE'
C.△E′EC∽△AFD
D.△AE′F是等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,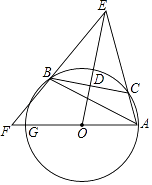
(1)点点同学通过画图和测量得到以下近似数据:
ɑ | 30° | 40° | 50° | 60° |
β | 120° | 130° | 140° | 150° |
γ | 150° | 140° | 130° | 120° |
猜想:β关于ɑ的函数表达式,γ关于ɑ的函数表达式,并给出证明:
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE,下列结论错误的是( ) 
A.BO=OH
B.DF=CE
C.DH=CG
D.AB=AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),C(0,3)点M、N为抛物线上的动点,过点M作MD∥y轴,交直线BC于点D,交x轴于点E.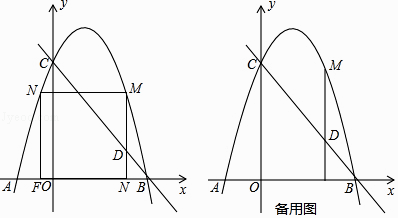
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点N作NF⊥x轴,垂足为点F,若四边形MNFE为正方形(此处限定点M在对称轴的右侧),求该正方形的面积;
(3)若∠DMN=90°,MD=MN,求点M的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)
(参考数据:sin67°≈ ![]() ,cos67°≈
,cos67°≈ ![]() ,tan67°≈
,tan67°≈ ![]() ,
, ![]() ≈1.73)
≈1.73)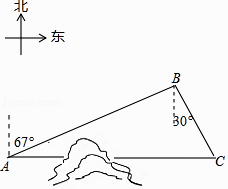
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线DE,交AC于点E,AC的反向延长线交⊙O于点F. 
(1)求证:DE⊥AC;
(2)若DE+EA=8,⊙O的半径为10,求AF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在矩形ABCD中,AB= ![]() ,BC=2,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是( )
,BC=2,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是( ) 
A.![]()
B.![]()
C.1
D.1.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com