
 ��1����ѧϰһ�κ�����ͼ��ʱ�����Ǹ��ݺ���ͼ��Ķ��壬��������ͼ��Ļ������裬����һ�κ�����ͼ��������������ͼ��Ļ������軭������y=2x+4��ͼ��
��1����ѧϰһ�κ�����ͼ��ʱ�����Ǹ��ݺ���ͼ��Ķ��壬��������ͼ��Ļ������裬����һ�κ�����ͼ��������������ͼ��Ļ������軭������y=2x+4��ͼ������ ��1��ȡ���㣬������㷨����ͼ�μ��ɣ�
��2�������ô���ϵ������y=kx+b��ת��Ϊ�����������⣮
�����x=16ʱ�ĺ���ֵ���ɽ�����⣮
��� �⣺��1����ֱ��y=2x+4��ȡ���㣨0��4���ͣ�-2��0���������㻭��ֱ���ɣ�ͼ����ͼ��ʾ��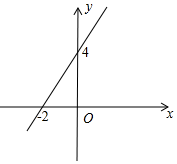

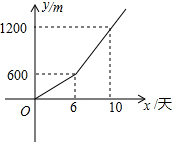
��2������y=kx+b����$\left\{\begin{array}{l}{6k+b=0}\\{10k+b=1200}\end{array}\right.$���$\left\{\begin{array}{l}{k=300}\\{b=-1800}\end{array}\right.$��
��y=300x-1800��
��x=16ʱ��y=300��16-1800=3000��
��ù�˾����̻�����·��Ϊ3000m��
�ʴ�Ϊ3000��
���� ���⿼��һ�κ�����Ӧ�ã�����ϵ��������㷨��ͼ��֪ʶ������Ĺؼ�����������һ�κ��������ʣ�ѧ�������ת��Ϊ�������������ڻ����⣮


 ��ʱѵ���������������ϵ�д�
��ʱѵ���������������ϵ�д� �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д� ����С����ҵ��ϵ�д�
����С����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
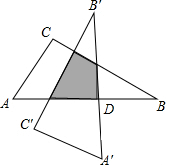 ��ͼ��Rt��ABC�У���C=90�㣬��A=60�㣬AC=6����б��AB���е�DΪ��ת���ģ�����������ΰ���ʱ�뷽����ת90��õ�Rt��A��B��C�䣬����ת������ֱ���������ص����ֵ����Ϊ��������
��ͼ��Rt��ABC�У���C=90�㣬��A=60�㣬AC=6����б��AB���е�DΪ��ת���ģ�����������ΰ���ʱ�뷽����ת90��õ�Rt��A��B��C�䣬����ת������ֱ���������ص����ֵ����Ϊ��������| A�� | 6 | B�� | 9 | C�� | 6$\sqrt{3}$ | D�� | 9$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | 7 | C�� | 8 | D�� | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��0�� | B�� | ��1��1�� | C�� | ��1��0�� | D�� | ��0��1�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com