
���� ��1�����������������Ҫx�죬���ҵ��������Ҫ2x�죬�������Ӻ���12����ɣ��ɵó����̣�������ɣ�
��2���г�����a��b�ķ��̼��ɽ�����⣮
��3��������ÿ��ķ��ñ��ˣ����������������ٺ�����ɷ�����С����������������������ɽ�����⣮
��� �⣺��1�����������������Ҫx�죬���ҵ��������Ҫ2x�죬
������ã�12����$\frac{1}{x}$+$\frac{1}{2x}$��=1��
��ã�x=18��
�����飬x=18�Ƿ��̵Ľ��ҷ������⣮
2x=36��
�𣺼�������������Ҫ18�죬�ҵ�������������Ҫ36�죮
��2��������$\frac{a}{18}$+$\frac{b}{36}$=1��
��b=36-2a��
��3����Ϊ��ÿ��Ĺ��̷�����0.6��Ԫ���Ҷ�ÿ��Ĺ��̷�����0.25��Ԫ����������������Ҫ18�죬�ҵ�������������Ҫ36�죮
��Ҫ16����ɣ�����ֻ�����Ӻ�������Ϊ�ҵ�ÿ��ķ���С��Ӧ��������������������a�죬�����ٺ���ǡ��������ɣ�
��$\frac{16}{36}$+$\frac{16-a}{18}$=1��
���a=6��
��������6�죬�����ٺ���10�죬������С��
���� ���⿼���˷�ʽ���̵�Ӧ�ã������Ĺؼ������δ֪�������÷���˼����⣬ע���ʽ������Ҫ���飬�����п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a7��a4=a3 | B�� | 5a2-3a=2a | C�� | 3a4•a2=3a8 | D�� | ��a3b2��2=a5b4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����ԽǷֱ���ȵ��ı�����ƽ���ı��� | |
| B�� | ����������ֱ�ǵ��ı����Ǿ��� | |
| C�� | �Խ����ഹֱ��ƽ���ı��������� | |
| D�� | һ��Ա�ƽ�е��ı�����ƽ���ı��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��4x-5y����-5y-4x�� | B�� | ��-4x+5y����-5y+4x�� | C�� | ��-4x-5y����5y+4x�� | D�� | ��4x-5y����5y-4x�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
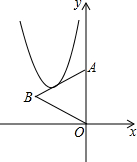 ��ͼ��������y=2x2+bx+c�Ķ����ڡ�OAB�ı�OB��AB���˶�����������O����A������֪A��0��2����B��-2��1����������˵��������ǣ�������
��ͼ��������y=2x2+bx+c�Ķ����ڡ�OAB�ı�OB��AB���˶�����������O����A������֪A��0��2����B��-2��1����������˵��������ǣ�������| A�� | 0��b��8 | B�� | 0��c��9 | C�� | 1+2c��b | D�� | b2��8c-16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
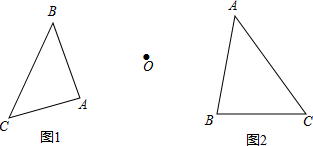 ��ͼ����֪��ABC����1��ͼ1���Ե�OΪ��ת����˳ʱ����ת60���ͼ�Σ�
��ͼ����֪��ABC����1��ͼ1���Ե�OΪ��ת����˳ʱ����ת60���ͼ�Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com