
【题目】如图,点![]() 在等边
在等边![]() 的边
的边![]() 上,
上,![]() ,射线
,射线![]() ,垂足为点
,垂足为点![]() ,点
,点![]() 是射线
是射线![]() 上一动点,点
上一动点,点![]() 是线段
是线段![]() 上一动点,当
上一动点,当![]() 的值最小时,
的值最小时,![]() ,则
,则![]() 的长为___________________.
的长为___________________.
【答案】13
【解析】
作出点M关于CD的对称点M1,然后过点M1作M1N⊥AB于N,交CD于点P,连接MP,根据对称性可得MP= M1P,MC= M1C,然后根据垂线段最短即可证出此时![]() 最小,然后根据等边三角形的性质可得AC=BC,∠B=60°,利用30°所对的直角边是斜边的一半即可求出BM1,然后求出BC即可求出AC.
最小,然后根据等边三角形的性质可得AC=BC,∠B=60°,利用30°所对的直角边是斜边的一半即可求出BM1,然后求出BC即可求出AC.
解:作出点M关于CD的对称点M1,然后过点M1作M1N⊥AB于N,交CD于点P,连接MP,如下图所示

根据对称性质可知:MP= M1P,MC= M1C
此时![]() =M1P+NP=M1N,根据垂线段最短可得此时
=M1P+NP=M1N,根据垂线段最短可得此时![]() 最小,且最小值为M1N的长
最小,且最小值为M1N的长
∵△ABC为等边三角形
∴AC=BC,∠B=60°
∴∠M1=90°-∠B=30°
∵![]() ,当
,当![]() 的值最小时,
的值最小时,![]() ,
,
∴在Rt△BM1N中,BM1=2BN=18
∴MM1= BM1-BM=10
∴MC= M1C=![]() MM1=5
MM1=5
∴BC=BM+MC=13
故答案为:13.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
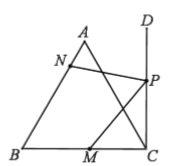
【题目】点I为△ABC的内心,连AI交△ABC的外接圆于点D,若AI=2CD,点E为弦AC的中点,连接EI,IC,若IC=6,ID=5,则IE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
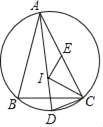
【题目】如图,已知∠BAC=60° ,∠B=80° ,DE垂直平分AC交BC于点D,交AC于点E.
(1)求∠BAD的度数;
(2)若AB=10,BC=12,求△ABD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
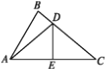
【题目】问题探究
(1)如图①,已知正方形ABCD的边长为4.点M和N分别是边BC、CD上两点,且BM=CN,连接AM和BN,交于点P.猜想AM与BN的位置关系,并证明你的结论.
(2)如图②,已知正方形ABCD的边长为4.点M和N分别从点B、C同时出发,以相同的速度沿BC、CD方向向终点C和D运动.连接AM和BN,交于点P,求△APB周长的最大值;
问题解决
(3)如图③,AC为边长为2![]() 的菱形ABCD的对角线,∠ABC=60°.点M和N分别从点B、C同时出发,以相同的速度沿BC、CA向终点C和A运动.连接AM和BN,交于点P.求△APB周长的最大值.
的菱形ABCD的对角线,∠ABC=60°.点M和N分别从点B、C同时出发,以相同的速度沿BC、CA向终点C和A运动.连接AM和BN,交于点P.求△APB周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
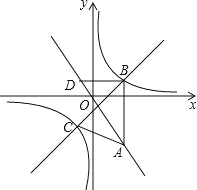
【题目】如图,在平面直角坐标系xOy中,点A(a,﹣![]() )在直线y=﹣
)在直线y=﹣![]() 上,AB∥y轴,且点B的纵坐标为1,双曲线y=
上,AB∥y轴,且点B的纵坐标为1,双曲线y=![]() 经过点B.
经过点B.
(1)求a的值及双曲线y=![]() 的解析式;
的解析式;
(2)经过点B的直线与双曲线y=![]() 的另一个交点为点C,且△ABC的面积为
的另一个交点为点C,且△ABC的面积为![]() .
.
①求直线BC的解析式;
②过点B作BD∥x轴交直线y=﹣![]() 于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
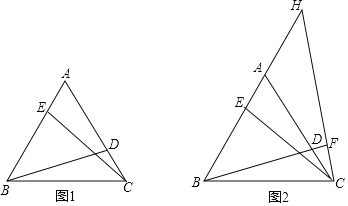
【题目】(1)如图1,点![]() 、
、![]() 分别是等边
分别是等边![]() 边
边![]() 、
、![]() 上的点,连接
上的点,连接![]() 、
、![]() ,若
,若![]() ,求证:
,求证:![]()
(2)如图2,在(1)问的条件下,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() 交
交![]() 延长线于点
延长线于点![]() ,.若
,.若![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
12×231=132×21,
13×341=143×31
23×352=253×32,
34×473=374×43,
62×286=682×26,
……
以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”
(1)根据上述各式反映的规律填空,使式子称为“数字对称等式”:
①52× = ×25
② ×396=693× ;
(2)设这类等式左边两位数的十位数字为a,个位数字为b,且2≤a+b≤9,写出表示“数字对称等式”一般规律的式子(含a,b),并证明;
(3)若(2)中a,b表示一个两位数,例如a=11,b=22,则1122×223311=113322×2211,请写出表示这类“数字对称等式”一般规律的式子(含a,b),并写出a+b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=![]() DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个村庄A、B在河CD的同侧,A、B两村到河的距离分别为AC=1千米,BD=3千米,CD=3千米.现要在河边CD上建造一水厂,向A、B两村送自来水.铺设水管的工程费用为每千米20000元,请你在CD上选择水厂位置O,使铺设水管的费用最省,并求出铺设水管的总费用W.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com