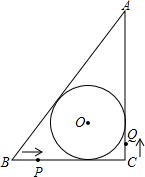
解:(1)作OD⊥AB于D,OE⊥AC于E,OF⊥BC于F,如图,⊙O的半径为Rcm,
∵⊙O是△ABC的内切圆,
∴OD=OE=OF,即点D、E、F为切点,
而∠C=90°,
∴四边形OECF为正方形,
∴CF=CE=OE=R,
∴BF=BC-CF=6-R,AE=8-R,
在△ABC中,∠C=90°,BC=6cm,CA=8cm,
∴AB=

=10cm,
∵BD=BF=6-E,AD=AE=8-R,
∴AB=BD+AD=6-R+8-R=10,
∴R=2,
即⊙O的半径为2cm;
(2)∵点Q移动到A所用的时间=

=4(秒),
而P、Q分别从B、C同时出发,
∴点P在BC上移动的距离=4×1=4cm,
∵CF=2cm,
∴BF=6cm-2cm=4cm,
∴P点移动到了F点,
而OF=2cm,
∴P点在⊙O上;
(3)设经过t秒,△PCQ的面积等于5cm
2,则BP=t,PC=6-t,CQ=2t,
根据题意得

(6-t)•2t=5,
解得t
1=1,t
2=5(舍去),
∴经过1秒,△PCQ的面积等于5cm
2.
分析:(1)作OD⊥AB于D,OE⊥AC于E,OF⊥BC于F,⊙O的半径为Rcm,根据切线的性质得OD=OE=OF,即点D、E、F为切点,易得四边形OECF为正方形,则CF=CE=OE=R,所以BF=6-R,AE=8-R,再利用勾股定理计算出AB=10cm,于是BD+AD=6-R+8-R=10,然后解方程即可得到R的值;
(2)先根据速度公式计算出点Q移动到A所用的时间为4秒,则点P在BC上移动的距离=4cm,易得P点移动到了F点,然后根据点与圆的位置关系可判断P点与⊙O是什么位置关系;
(3)设经过t秒,△PCQ的面积等于5cm
2,根据三角形面积公式得到

(6-t)•2t=5,然后解一元二次方程求出t,然后根据Q移动到A时,移动停止可确定的值.
点评:本题考查了圆的综合题:熟练掌握圆的切线的性质、切线长定理和点与圆的位置关系;会利用勾股定理进行几何计算;能运用方程的思想解决问题.

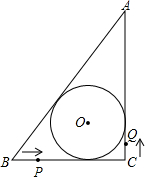 拓展探索.
拓展探索. 解:(1)作OD⊥AB于D,OE⊥AC于E,OF⊥BC于F,如图,⊙O的半径为Rcm,
解:(1)作OD⊥AB于D,OE⊥AC于E,OF⊥BC于F,如图,⊙O的半径为Rcm, =10cm,
=10cm, =4(秒),
=4(秒), (6-t)•2t=5,
(6-t)•2t=5, (6-t)•2t=5,然后解一元二次方程求出t,然后根据Q移动到A时,移动停止可确定的值.
(6-t)•2t=5,然后解一元二次方程求出t,然后根据Q移动到A时,移动停止可确定的值.

 拓展探索.
拓展探索.