

分析 (1)直接利用直角三角形的性质表示出HC,以及AH的长进而求出答案;
(2)分别利用①AB=AD=2,∠BAD=60°,②BC=BD=2$\sqrt{3}$+2,∠BCD=60°,③AD=CD=AC=$\sqrt{2}$HC=3$\sqrt{2}$+$\sqrt{6}$,∠ADC=60°分别求出答案;
(3)首先延长BC至点E,使CE=CD=4,进而求出△ACD≌△BED(SSS),进而求出△ABD是等边三角形,得出四边形ABCD是“准筝形”.
解答  解:(1)如图2-1,设BH=x,
解:(1)如图2-1,设BH=x,
∵∠ABC=120°,CH是△ABC的高线,
∴∠BCH=30°,
∴HC=$\sqrt{3}$x,
又∵∠A=45°,
∴HA=HC,
∵AB=2,∴$\sqrt{3}$x=2+x,
解得:x=$\sqrt{3}$+1,
∴HC=$\sqrt{3}$x=3+$\sqrt{3}$;
(2)在(1)条件下,四边形ABCD的面积是:3+2$\sqrt{3}$,9+5$\sqrt{3}$或12+7$\sqrt{3}$.
①如图2-2,AB=AD=2,∠BAD=60°,
作CG垂直BD的延长线于点G,则BD=2,
易得:∠CBG=60°=∠CBH,
在△CBG和△CBH中
∵$\left\{\begin{array}{l}{∠CGB=∠CHB}\\{∠CBG=∠CBH}\\{BC=BC}\end{array}\right.$,
∴△CBG≌△CBH(AAS),
∴GC=HC=3+$\sqrt{3}$,
作AK⊥BD于K,则易得:AK=$\sqrt{3}$,
∴S△ABD=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$,S△CBD=$\frac{1}{2}$×2×(3+$\sqrt{3}$)=3+$\sqrt{3}$,
∴S四边形ABCD=3+2$\sqrt{3}$;
②如图2-3,BC=BD=2$\sqrt{3}$+2,∠BCD=60°,
作CG垂直BD的延长线于点G,则BD=2$\sqrt{3}$+2,
易得:CG=3+$\sqrt{3}$,易得:AK=$\sqrt{3}$,
∴S△BCD=$\frac{1}{2}$×(3+$\sqrt{3}$)(2+2$\sqrt{3}$)=4$\sqrt{3}$+6,S△ABD=$\frac{1}{2}$×$\sqrt{3}$×(2+2$\sqrt{3}$)=3+$\sqrt{3}$,
∴S四边形ABCD=9+5$\sqrt{3}$;
③如图2-4,AD=CD=AC=$\sqrt{2}$HC=3$\sqrt{2}$+$\sqrt{6}$,∠ADC=60°,
作DM⊥AC于M,
易得:DM=$\frac{\sqrt{3}}{2}$(3$\sqrt{2}$+$\sqrt{6}$)=$\frac{3}{2}$($\sqrt{6}$+$\sqrt{2}$),
∴S△ABC=$\frac{1}{2}$×2×(3+$\sqrt{3}$)=3+$\sqrt{3}$,
S△ADC=$\frac{1}{2}$×(3$\sqrt{2}$+$\sqrt{6}$)×$\frac{3}{2}$($\sqrt{6}$+$\sqrt{2}$)=6$\sqrt{3}$+9,
∴S四边形ABCD=12+7$\sqrt{3}$;
(3)四边形ABCD是“准筝形”.
理由:如图3,延长BC至点E,使CE=CD=4,连结DE,
∵∠BCD=120°,
∴∠DCE=60°,
∴△DCE是等边三角形,
∴ED=CD=4,∠CDE=60°,
∵BC=2,CE=CD=4,AC=6,
∴AC=EB,
在△ACD和△BED中,
∵$\left\{\begin{array}{l}{AD=BD}\\{AC=EB}\\{CD=ED}\end{array}\right.$,
∴△ACD≌△BED(SSS),
∴∠ADC=∠BDE,
∴∠ADB=∠CDE=60°,
∴△ABD是等边三角形,
∴AB=AD,∠BAD=60°,
∴四边形ABCD是“准筝形”.
点评 此题主要考查了四边形综合以及全等三角形的判定与性质以及等边三角形的性质和直角三角形的性质等知识,正确利用“准筝形”的定义结合分类讨论求出是解题关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
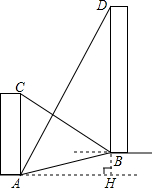 如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是$1:2\sqrt{3}$.从点A测得楼BD顶部D处的仰角是60°,从点B测得楼AC顶部C处的仰角是30°,楼BD的自身高度比楼AC高12m.求楼AC与楼BD之间的水平距离.(结果保留根号)
如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是$1:2\sqrt{3}$.从点A测得楼BD顶部D处的仰角是60°,从点B测得楼AC顶部C处的仰角是30°,楼BD的自身高度比楼AC高12m.求楼AC与楼BD之间的水平距离.(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com