
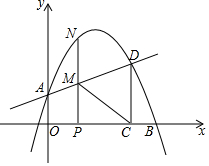
 ��ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+1��y���ڵ�A����x���������ڵ�B��4��0�������A���ֱ���ཻ����һ��D��3��$\frac{5}{2}$��������D��DC��x�ᣬ����ΪC��
��ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+1��y���ڵ�A����x���������ڵ�B��4��0�������A���ֱ���ཻ����һ��D��3��$\frac{5}{2}$��������D��DC��x�ᣬ����ΪC������ ��1����B��4��0������D��3��$\frac{5}{2}$������y=ax2+bx+1���ɵó������ߵĽ���ʽ��
��2�����ú�t�Ĵ���ʽ��ʾP��M���꣬�ٸ��������ε������ʽ�����PCM�������t�ĺ�����ϵʽ��Ȼ�������䷽���������PCM��������ֵ��
��3�����ı���DCMNΪƽ���ı��Σ�����MN=DC���ʿɵó�����t�Ķ�Ԫһ�η��̣��ⷽ�̼��ɵõ����ۣ�
��� �⣺��1���ѵ�B��4��0������D��3��$\frac{5}{2}$��������y=ax2+bx+1�еã�$\left\{\begin{array}{l}{16a+4b+1=0}\\{9a+3b+1=\frac{5}{2}}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=-\frac{3}{4}}\\{b=\frac{11}{4}}\end{array}\right.$��
�������ߵı���ʽΪy=-$\frac{3}{4}$x2+$\frac{11}{4}$x+1��
��2����ֱ��AD�Ľ���ʽΪy=kx+b��
��A��0��1����D��3��$\frac{5}{2}$����
��$\left\{\begin{array}{l}{b=1}\\{3k+b=\frac{5}{2}}\\{\;}\end{array}\right.$��
��$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=1}\end{array}\right.$��
��ֱ��AD�Ľ���ʽΪy=$\frac{1}{2}$x+1��
��P��t��0����
��M��t��$\frac{1}{2}$t+1����
��PM=$\frac{1}{2}$t+1��
��CD��x�ᣬ
��PC=3-t��
��S��PCM=$\frac{1}{2}$PC•PM=$\frac{1}{2}��$��3-t����$\frac{1}{2}$t+1����
��S��PCM=-$\frac{1}{4}$t2+$\frac{1}{4}$t+$\frac{3}{2}$=-$\frac{1}{4}$��t-$\frac{1}{2}$��2+$\frac{25}{16}$��
���PCM��������ֵ��$\frac{25}{16}$��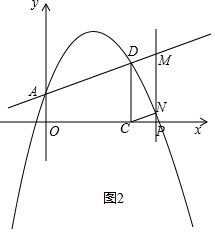
��3����OP=t��
���M��N�ĺ�����Ϊt��
��M��t��$\frac{1}{2}$t+1����N��t��-$\frac{3}{4}$t2+$\frac{11}{4}$t+1����
��|MN|=|-$\frac{3}{4}$t2+$\frac{11}{4}$t+1-$\frac{1}{2}$t-1|=|-$\frac{3}{4}$t2+$\frac{9}{4}$t|��CD=$\frac{5}{2}$��
��ͼ1������Ե�M��C��D��NΪ������ı�����ƽ���ı��Σ�
��MN=CD����-$\frac{3}{4}$t2+$\frac{9}{4}$t=$\frac{5}{2}$��
�ߡ�=-39��
���-$\frac{3}{4}$t2+$\frac{9}{4}$t=$\frac{5}{2}$��ʵ������
�����t��
��ͼ2������Ե�M��C��D��NΪ������ı�����ƽ���ı��Σ�
��MN=CD����$\frac{3}{4}$t2-$\frac{9}{4}$t=$\frac{5}{2}$��
��t=$\frac{9+\sqrt{201}}{6}$������ֵ��ȥ����
�൱t=$\frac{9+\sqrt{201}}{6}$ʱ���Ե�M��C��D��NΪ������ı�����ƽ���ı��Σ�
���� ���⿼����Ƕ��κ��������ʡ�����ϵ������������ʽ��ƽ���ı��ε��ж�����ȷ������κ����Ľ���ʽ�������䷽����һ��ʽ��Ϊ����ʽ�������������ֵ�ǽ���Ĺؼ���ע�����ε��ж�������������ã�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����Rt��ABC��ֱ�Ƕ���C˳ʱ����ת90�㣬�õ���A��B��C������AA�䣬����1=25�㣬���BAA��Ķ����ǣ�������
��ͼ����Rt��ABC��ֱ�Ƕ���C˳ʱ����ת90�㣬�õ���A��B��C������AA�䣬����1=25�㣬���BAA��Ķ����ǣ�������| A�� | 55�� | B�� | 60�� | C�� | 65�� | D�� | 70�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����A���мס��������洬���״��ر�ƫ��60��ķ�����6����/ʱ���ٶ�ǰ�����Ҵ�����ƫ��30��ķ�����8����/ʱ���ٶ�ǰ����2Сʱ��ֱ�B��C��������B��C�����ľ��룮
��ͼ����A���мס��������洬���״��ر�ƫ��60��ķ�����6����/ʱ���ٶ�ǰ�����Ҵ�����ƫ��30��ķ�����8����/ʱ���ٶ�ǰ����2Сʱ��ֱ�B��C��������B��C�����ľ��룮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com