
【题目】如图,点A在直线l上,点Q沿着直线l以3厘米/秒的速度由点A向右运动,以AQ为边作Rt△ABQ,使∠BAQ=90°,tan∠ABQ= ![]() ,点C在点Q右侧,CQ=1厘米,过点C作直线m⊥l,过△ABQ的外接圆圆心O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=
,点C在点Q右侧,CQ=1厘米,过点C作直线m⊥l,过△ABQ的外接圆圆心O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF= ![]() CD,以DE、DF为邻边作矩形DEGF.设运动时间为t秒.
CD,以DE、DF为邻边作矩形DEGF.设运动时间为t秒.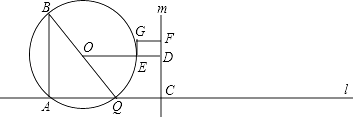
(1)直接用含t的代数式表示BQ、DF;
(2)当0<t<1时,求矩形DEGF的最大面积;
(3)点Q在整个运动过程中,当矩形DEGF为正方形时,求t的值.
【答案】
(1)解:∵点Q沿着直线l以3厘米/秒的速度由点A向右运动,运动时间为t秒.
∴AQ=3t,
∵∠BAQ=90°,tan∠ABQ= ![]() =
= ![]() ,
,
∴AB=4t,
∴BQ= ![]() =5t,
=5t,
作OM⊥AQ于M,则AM=QM= ![]() AQ=1.5t,CD=OM,
AQ=1.5t,CD=OM,
∴OM是△ABQ的中位线,
∴CD=OM= ![]() AB=2t,
AB=2t,
∴DF= ![]() CD=
CD= ![]() t
t
(2)解:设矩形DEGF的面积为S,
∵OE=OB= ![]() BQ=
BQ= ![]() t,OD=QM+CQ=
t,OD=QM+CQ= ![]() t+1,
t+1,
∴DE=OD﹣OE= ![]() t+1﹣
t+1﹣ ![]() t=1﹣t,
t=1﹣t,
∴ ![]() ,
,
∴当t= ![]() 时,矩形DEGF的最大面积为
时,矩形DEGF的最大面积为 ![]()
(3)解:当矩形DEGF为正方形时,则DE=DF,分两种情况:
①当0<t<1时,如图1所示:
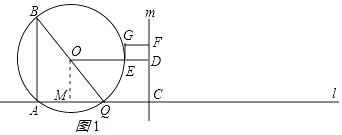
DE=1﹣t,
∴1﹣t= ![]() t,
t,
解得:t= ![]() ;
;
②当t≥1时,如图2所示:
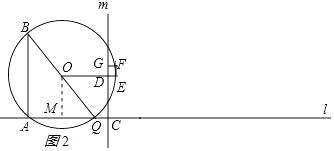
DE=t﹣1,
∴t﹣1= ![]() t,
t,
解得:t=3;
综上所述:当矩形DEGF为正方形时,t的值为 ![]() 或3.
或3.
【解析】(1)由已知得出AQ=3t,由三角函数求出AB=4t,再由勾股定理求出BQ= 5t,作OM⊥AQ于M,则AM=QM= ![]() AQ=1.5t,CD=OM,由三角形的中位线定理得出CD=OM=
AQ=1.5t,CD=OM,由三角形的中位线定理得出CD=OM= ![]() AB=2t,进而得出结论;
AB=2t,进而得出结论;
(2)设矩形DEGF的面积为S,OE= ![]() t,OD=QM+CQ=
t,OD=QM+CQ= ![]() t+1,
t+1,
∴DE=OD﹣OE= ![]() t+1﹣
t+1﹣ ![]() t=1﹣t,由矩形的面积得出s是t的二次函数,即可得出答案;
t=1﹣t,由矩形的面积得出s是t的二次函数,即可得出答案;
(3)当矩形DEGF为正方形时,则DE=DF,分两种情况:①当0<t<1时,如图1所示得出方程,解方程即可;②当t≥1时,如图2所示:DE=t﹣1,得出方程,解方程即可。
【考点精析】解答此题的关键在于理解二次函数的最值的相关知识,掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】你会求(a﹣1)(a2012+a2011+a2010+…+a2+a+1)的值吗?这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律:
![]() ,
,
![]() ,
,
![]() ,
,
(1)由上面的规律我们可以大胆猜想,得到(a﹣1)(a2014+a2013+a2012+…+a2+a+1)=
利用上面的结论,求:
(2)22014+22013+22012+…+22+2+1的值是 .
(3)求52014+52013+52012+…+52+5+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC =3,BC =4,AB=5,BD平分∠ABC,如果M、N分别为BD、BC上的动点,那么CM+MN的最小值是____.
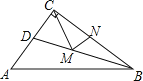
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图2形状拼成一个正方形.
的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图2形状拼成一个正方形.
(1)请用两种不同方法,求图2中阴影部分的面积(不用化简)
方法1:____________________
方法2:____________________
(2)观察图2,写出![]() ,
,![]() ,
,![]() 之间的等量关系,并验证;
之间的等量关系,并验证;

(3)根据(2)题中的等量关系,解决如下问题:
①若![]() ,
,![]() ,求
,求![]() 的值;
的值;
②若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,∠AEO=∠C,OE交BC于点F.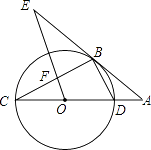
(1)求证:OE∥BD;
(2)当⊙O的半径为5,sin∠DBA= ![]() 时,求EF的长.
时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
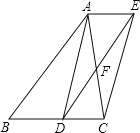
【题目】如图,已知点D是△ABC的边BC的中点,直线AE∥BC,过点D作直线DE∥AB,分别交AE、AC于点E、F。
(1)求证:四边形ADCE是平行四边形;
(2)如果四边形ADCE是矩形,△ABC应满足什么条件?并说明理由;
(3)如果四边形ADCE是菱形,直接写出△ABC应满足的条件是 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() (x>0)的图象与一次函数y=3x的图象相交于点A,其横坐标为2.
(x>0)的图象与一次函数y=3x的图象相交于点A,其横坐标为2.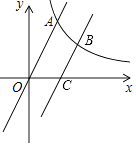
(1)求k的值;
(2)点B为此反比例函数图象上一点,其纵坐标为3.过点B作CB∥OA,交x轴于点C,直接写出线段OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:观察下面由“※”组成的图案和算式,解答问题:
1+3=4=(![]() )2=22
)2=22
1+3+5=9=(![]() )2=32
)2=32
1+3+5+7=16=(![]() )2=42
)2=42
…
问题解决:
(1)试猜想1+3+5+7+9…+49的结果为 ;
(2)若n 表示正整数,请用含n 的代数式表示1+3+5+7+9+…+(2n﹣1)+(2n+1) 的结果.
问题拓展:
(3)请用上述规律计算:1017+1019+…+2017+2019.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com