
【题目】完成下面的证明
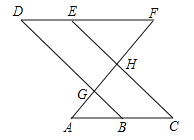
如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D.
求证:∠A=∠F.

证明:∵∠AGB=∠EHF
∠AGB=___________(对顶角相等)
∴∠EHF=∠DGF
∴DB∥EC(____________________________________)
∴∠_________=∠DBA(________________________________)
又∵∠C=∠D
∴∠DBA=∠D
∴DF∥_______(__________________________________)
∴∠A=∠F(__________________________________).
【答案】 ∠DGF 同位角相等,两直线平行 C 两直线平行,同位角相等 AC 内错角相等,两直线平行 两直线平行,内错角相等
【解析】试题分析:根据对顶角相等推知同位角∠EHF=∠DGF,从而证得两直线DB∥EC;然后由平行线的性质知内错角∠DBA=∠D,即可根据平行线的判定定理推知两直线DF∥AC;最后由平行线的性质(两直线平行,内错角相等)证得∠A=∠F.
试题解析:解:∵∠AGB=∠EHF,∠AGB=∠DGF(对顶角相等),∴∠EHF=∠DGF
,∴DB∥EC(同位角相等,两直线平行),∴∠C=∠DBA ( 两直线平行,同位角相等);
又∵∠C=∠D(已知),∴∠DBA=∠D(等量代换),∴DF∥AC(内错角相等,两直线平行),∴∠A=∠F(两直线平行,内错角相等).


科目:初中数学 来源: 题型:
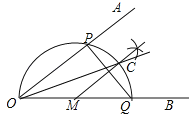
【题目】已知∠AOB,作图.
步骤1:在OB上任取一点M,以点M为圆心,MO长为半径画半圆,分别交OA、OB于点P、Q;
步骤2:过点M作PQ的垂线交 ![]() 于点C;
于点C;
步骤3:画射线OC.
则下列判断:①![]() =
=![]() ;②MC∥OA;③OP=PQ;④OC平分∠AOB,其中正确的个数为( )
;②MC∥OA;③OP=PQ;④OC平分∠AOB,其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,最适合采用普查的是( )
A.对某班全体学生出生月份的调查B.对全国中学生节水意识的调查
C.对某批次灯泡使用寿命的调查D.对山西省初中学生每天阅读时间的调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC.中,AB=BC,将△ABC绕点B顺时针旋转α度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF=α,②A1E=CF,③DF=FC,④A1F=CE.其中正确的是 (写出正确结论的序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
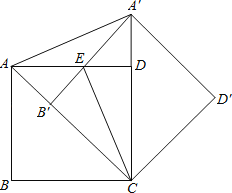
【题目】如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线AC上,点A′落在CD的延长线上),A′B′交AD于点E,连接AA′、CE.
求证:(1)△ADA′≌△CDE;
(2)直线CE是线段AA′的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
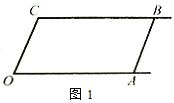
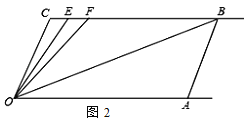
【题目】如图1,已知射线CB∥OA,∠C=∠OAB,
(1)求证:AB∥OC;
(2)如图2,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
①当∠C=110°时,求∠EOB的度数.
②若平行移动AB,那么∠OBC :∠OFC的值是否随之发生变化?若变化,找出变
化规律;若不变,求出这个比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
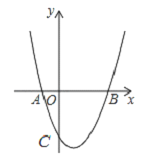
【题目】如图,已知抛物线y=x2+bx+c经过A(-1,0)、B(3,0)两点,点C是抛物线与y轴的交点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
(3)在抛物线的对称轴上是否存在点M,使△BCM是等腰三角形,若存在请直接写出点M坐标,若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com