
【题目】已知:如图,抛物线y=a(x﹣1)2+c与x轴交于点A( ![]() ,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P′(1,3)处.
,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P′(1,3)处. 
(1)求原抛物线的解析式;
(2)学校举行班徽设计比赛,九年级5班的小明在解答此题时顿生灵感:过点P′作x轴的平行线交抛物线于C,D两点,将翻折后得到的新图象在直线CD以上的部分去掉,设计成一个“W”型的班徽,“5”的拼音开头字母为W,“W”图案似大鹏展翅,寓意深远;而且小明通过计算惊奇的发现这个“W”图案的高与宽(CD)的比非常接近黄金分割比 ![]() (约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据:
(约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据: ![]() ,
, ![]() ,结果可保留根号)
,结果可保留根号)
【答案】
(1)解:∵P与P′(1,3)关于x轴对称,
∴P点坐标为(1,﹣3);
∵抛物线y=a(x﹣1)2+c过点A( ![]() ,0),顶点是P(1,﹣3),
,0),顶点是P(1,﹣3),
∴ ![]() ;
;
解得 ![]() ;
;
则抛物线的解析式为y=(x﹣1)2﹣3,
即y=x2﹣2x﹣2
(2)解:∵CD平行x轴,P′(1,3)在CD上,
∴C、D两点纵坐标为3;
由(x﹣1)2﹣3=3,
解得: ![]() ,
, ![]() ,
,
∴C、D两点的坐标分别为( ![]() ,3),(
,3),( ![]() ,3)
,3)
∴CD= ![]()
∴“W”图案的高与宽(CD)的比= ![]() (或约等于0.6124)
(或约等于0.6124)
【解析】(1)利用P与P′(1,3)关于x轴对称,得出P点坐标,利用待定系数法求出二次函数的解析式即可;(2)根据已知得出C,D两点坐标,进而得出“W”图案的高与宽(CD)的比.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE,BE,BE⊥AE,延长AE交BC的延长线于点F.求证: 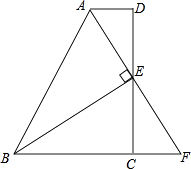
(1)FC=AD;
(2)AB=BC+AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图用点A(3,1)表示放置3个胡萝卜、1棵青菜,点B(2,3)表示放置2个胡萝卜、3棵青菜.

(1)请你写出其他各点C,D,E,F所表示的意义;
(2)若一只兔子从A到达B(顺着方格线走),有以下几条路可以选择:①A→C→D→B;②A→F→D→B;③A→F→E→B,帮可爱的小白兔选一条路,使它吃到的食物最多.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五子连珠棋和象棋、围棋一样,深受广大棋友的喜爱,其规则是:15×15的正方形棋盘中,由黑方先行,轮流弈子,在任一方向上连成五子者为胜.如图是两个五子棋爱好者甲和乙的对弈图(甲执黑子先行,乙执白子后走),观察棋盘思考:若A点的位置记作(8,4),甲必须在哪个位置上落子,才不会让乙在短时间内获胜?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.

情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:

你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在比例尺是1:4000的成都市城区地图上,位于锦江区的九眼桥的长度约为3cm,它的实际长度用科学记数法表示为( )
A.12×103cmB.1.2×102mC.1.2×104mD.0.12×105cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com