Question

如图，线段AD＝5，⊙A的半径为1，C为⊙A上一动点，CD的垂直平分线分别交CD，AD于点E，B，连接BC，AC，构成△ABC，设AB＝x．

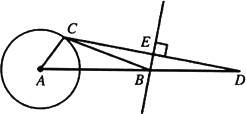
(1)求x的取值范围；

(2)若△ABC为直角三角形，则x＝________；

(3)设△ABC的面积的平方为W，求W的最大值．

Answer 1

答案：
解析：

分析：(1)由AD＝5，AB＝x，BE垂直平分CD，可得BC＝BD＝5－x，又由，⊙A的半径为1，根据三角形三边关系，即可求得x的取值范围； 　　(2)分别从若AB是斜边与BC是斜边去分析，利用勾股定理的知识，借助于方程即可求得x的值； 　　(3)在△ABC中，作CF⊥AB于F，设CF＝h，AF＝m，则W＝(xh)2＝x2h2，由AC2－AF2＝BC2－BF2，则1－m2＝(5－x)2－(x－m)2，分别从2.4＜x＜3时与2＜x≤2.4去分析，即可求得答案． 　　解答：解：(1)∵AD＝5，AB＝x，BE垂直平分CD， 　　∴BC＝BD＝5－x，在△ABC中，AC＝1， 　　∴(5－x)－1＜x＜1＋(5－x)， 　　解得：2＜x＜3； 　　(2)∵△ABC为直角三角形， 　　若AB是斜边，则AB2＝AC2＋BC2， 　　即x2＝(5－x)2＋1， 　　∴x＝2.6； 　　若BC是斜边，则BC2＝AB2＋AC2， 　　即(5－x)2＝x2＋1， 　　∴x＝2.4． 　　故答案为：2.4或2.6． 　　(3)在△ABC中，作CF⊥AB于F，设CF＝h，AF＝m，则W＝(xh)2＝x2h2， 　　①如图，当2.4＜x＜3时，AC2－AF2＝BC2－BF2，则1－m2＝(5－x)2－(x－m)2， 　　得：m＝， 　　∴h2＝1－m2＝， 　　∴W＝x2h2＝－6x2＋30x－36， 　　即W＝－6(x－)2＋， 　　当x＝2.5时(满足2.4＜x＜3)，W取最大值1.5； 　　②当2＜x≤2.4时，同理可得：W＝－6x2＋30x－36＝－6(x－)2＋， 　　当x＝2.4时，W取最大值1.44＜1.5， 　　综合①②得，W的最大值为1.5． 　　点评：此题考查了三角形三边关系，线段垂直平分线的性质，直角三角形的性质以及二次函数的最值问题等知识．此题综合性很强，难度适中，解题的关键是注意数形结合与分类讨论思想的应用．

提示：

考点：二次函数的最值；三角形三边关系；线段垂直平分线的性质；勾股定理．