
【题目】已知正方形![]() 中
中![]() 与
与![]() 交于
交于![]() 点,点
点,点![]() 在线段
在线段![]() 上,作直线
上,作直线![]() 交直线
交直线![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,设直线
,设直线![]() 交
交![]() 于
于![]() .
.

(1)如图,当![]() 在线段
在线段![]() 上时,求证:
上时,求证:![]() ;
;
(2)如图2,当![]() 在线段
在线段![]() 上,连接
上,连接![]() ,当
,当![]() 时,求证:
时,求证:![]() ;
;
(3)在图3,当![]() 在线段
在线段![]() 上,连接
上,连接![]() ,当
,当![]() 时,求证:
时,求证:![]() .
.
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】(1)先判断出OD=OA,∠AOM=∠DON,再利用同角的余角相等判断出∠ODN=∠OAM,判断出△DON≌△AOM即可得出结论;
(2)先判断出四边形DENM是菱形,进而判断出∠BDN=22.5°,即可判断出∠AMB=67.5°,即可得出结论;
(3)设CE=a,进而表示出EN=CE=a,CN=![]() a,设DE=b,进而表示AD=a+b,根据勾股定理得,AC=
a,设DE=b,进而表示AD=a+b,根据勾股定理得,AC=![]() (a+b),同(1)的方法得,∠OAM=∠ODN,得出∠EDN=∠DAE,进而判断出△DEN∽△ADE,得出
(a+b),同(1)的方法得,∠OAM=∠ODN,得出∠EDN=∠DAE,进而判断出△DEN∽△ADE,得出![]() ,进而得出a=
,进而得出a=![]() b,即可表示出CN=
b,即可表示出CN=![]() b,AC=
b,AC=![]() b,AN=AC﹣CN=
b,AN=AC﹣CN=![]() b,即可得出结论.
b,即可得出结论.
(1)∵正方形ABCD的对角线AC,BD相交于O,
∴OD=OA,∠AOM=∠DON=90°,
∴∠OND+∠ODN=90°,
∵∠ANH=∠OND,
∴∠ANH+∠ODN=90°,
∵DH⊥AE,
∴∠DHM=90°,
∴∠ANH+∠OAM=90°,
∴∠ODN=∠OAM,
∴△DON≌△AOM,
∴OM=ON;
(2)连接MN,
∵EN∥BD,
∴∠ENC=∠DOC=90°,∠NEC=∠BDC=45°=∠ACD,
∴EN=CN,同(1)的方法得,OM=ON,
∵OD=OD,
∴DM=CN=EN,
∵EN∥DM,
∴四边形DENM是平行四边形,
∵DN⊥AE,
∴DENM是菱形,
∴DE=EN,
∴∠EDN=∠END,
∵EN∥BD,
∴∠END=∠BDN,
∴∠EDN=∠BDN,
∵∠BDC=45°,
∴∠BDN=22.5°,
∵∠AHD=90°,
∴∠AMB=∠DME=90°﹣∠BDN=67.5°,
∵∠ABM=45°,
∴∠BAM=67.5°=∠AMB,
∴BM=AB;
(3)设CE=a(a>0)
∵EN⊥CD,
∴∠CEN=90°,
∵∠ACD=45°,
∴∠CNE=45°=∠ACD,
∴EN=CE=a,
∴CN=![]() a,
a,
设DE=b(b>0),
∴AD=CD=DE+CE=a+b,
根据勾股定理得,AC=![]() AD=
AD=![]() (a+b),
(a+b),
同(1)的方法得,∠OAM=∠ODN,
∵∠OAD=∠ODC=45°,
∴∠EDN=∠DAE,∵∠DEN=∠ADE=90°,
∴△DEN∽△ADE,
∴![]() ,
,
∴![]() ,
,
∴a=![]() b(已舍去不符合题意的)
b(已舍去不符合题意的)
∴CN=![]() a=
a=![]() b,AC=
b,AC=![]() (a+b)=
(a+b)=![]() b,
b,
∴AN=AC﹣CN=![]() b,
b,
∴AN2=2b2,ACCN=![]() b
b![]() b=2b2
b=2b2
∴AN2=ACCN.


科目:初中数学 来源: 题型:
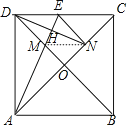
【题目】如图已知:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.求证:

(1)∠ECD=∠EDC;
(2)OE是CD的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
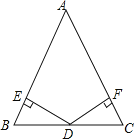
(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,先填空后证明.
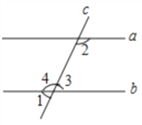
已知: ∠1+∠2=180° 求证:a∥b.
证明:∵ ∠1=∠3(_____),∠1+∠2=180°(_____),
∴ ∠3+∠2=180°(______).
∴ a∥b(_____).
请你再写出一种证明方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°.
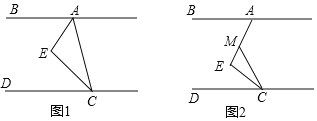
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
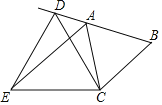
【题目】如图,等边△ABC的边长为4,D是线段BA延长线上的一点,以线段CD为边向CD的左侧作等边△CDE,连接AE.
(1)△ABC的面积S△ABC= ;
(2)求证:△ACE≌△BCD;
(3)若四边形ABCE的面积为10![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABC 的顶点 A (-2,0),点 B,C分别在x轴和y轴的正半轴上,∠ACB=90°,∠BAC=60°
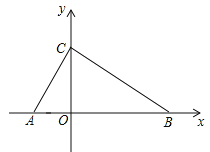
(1)求点 B 的坐标;
(2)点 P 为 AC延长线上一点,过 P 作PQ∥x轴交 BC 的延长线于点 Q ,若点 P 的横坐标为t,线段PQ的长为d,请用含t的式子表示d;
(3) 在(2)的条件下,当PA=![]() d时,E是线段CQ上一点,连接OE,BP,若OE=BP,求∠APB-∠OEB的度数..
d时,E是线段CQ上一点,连接OE,BP,若OE=BP,求∠APB-∠OEB的度数..
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=![]() =
=![]() ,根据上述角的余切定义,解下列问题:
,根据上述角的余切定义,解下列问题:
(1)如图1,若BC=3,AB=5,则ctanB= ;
(2)ctan60°= ;
(3)如图2,已知:△ABC中,∠B是锐角,ctan C=2,AB=10,BC=20,试求∠B的余弦cosB的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com