
 ,
, )
)
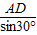 求出AP;若甲车司机手机要有信号,其距P必须等于或小于30千米,即让AP减去30千米再除以甲车的速度就可知道甲车司机手机什么时候有信号了.
求出AP;若甲车司机手机要有信号,其距P必须等于或小于30千米,即让AP减去30千米再除以甲车的速度就可知道甲车司机手机什么时候有信号了.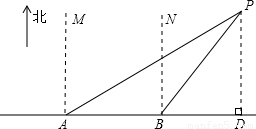
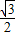 =10
=10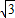 (千米)
(千米)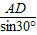 =20
=20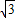 (千米);
(千米);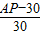 小时有信号,
小时有信号,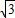 -30)÷30≈0.155(小时),合9分钟.
-30)÷30≈0.155(小时),合9分钟.

 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
| 2 |
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ,
, )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com