

|
|
| 3 |
| ||
| 3 |
|-
| ||||||
|


科目:初中数学 来源: 题型:
 假期测量超然楼的高度,在大明湖边一块平地上,甲和乙两名同学利用所带工具测量了一些数据,下面是他们的一段对话:
假期测量超然楼的高度,在大明湖边一块平地上,甲和乙两名同学利用所带工具测量了一些数据,下面是他们的一段对话:| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 中国拥有五千年悠久的历史,也出现了许多杰出的人物.例如,中国古代数学家-----宋朝赵爽用弦图(如图1)验证了一条几何学重要的定理:直角三角形两直角边的平方和等于斜边的平方,即a2+b2=c2.这就是著名的“勾股定理”.
中国拥有五千年悠久的历史,也出现了许多杰出的人物.例如,中国古代数学家-----宋朝赵爽用弦图(如图1)验证了一条几何学重要的定理:直角三角形两直角边的平方和等于斜边的平方,即a2+b2=c2.这就是著名的“勾股定理”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 中国拥有五千年悠久的历史,也出现了许多杰出的人物.例如,中国古代数学家-----宋朝赵爽用弦图(如图1)验证了一条几何学重要的定理:直角三角形两直角边的平方和等于斜边的平方,即a2+b2=c2.这就是著名的“勾股定理”.
中国拥有五千年悠久的历史,也出现了许多杰出的人物.例如,中国古代数学家-----宋朝赵爽用弦图(如图1)验证了一条几何学重要的定理:直角三角形两直角边的平方和等于斜边的平方,即a2+b2=c2.这就是著名的“勾股定理”.查看答案和解析>>
科目:初中数学 来源:2012年山东省济南市历下区中考数学一模试卷(解析版) 题型:解答题
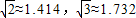 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com