
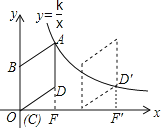
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数![]() (k>0,x>0)的图象上,点D的坐标为(
(k>0,x>0)的图象上,点D的坐标为(![]() ,2).
,2).
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的一个顶点恰好落在函数![]() (k>0,x>0)的图象上时,求菱形ABCD平移的距离;
(k>0,x>0)的图象上时,求菱形ABCD平移的距离;

【答案】(1)k=![]() ;(2)菱形ABCD平移的距离为
;(2)菱形ABCD平移的距离为![]() 或
或![]() 时,菱形的一个顶点恰好落在函数图像上.
时,菱形的一个顶点恰好落在函数图像上.
【解析】试题分析: (1)过点D作x轴的垂线,垂足为F,首先得出A点坐标,再利用反比例函数图象上点的坐标性质得出即可;
(2)将菱形ABCD沿x轴正方向平移,使得点D落在函数y=![]() (x>0)的图象D′点处,得出点D′的纵坐标为2,求出其横坐标,进而得出菱形ABCD平移的距离.
(x>0)的图象D′点处,得出点D′的纵坐标为2,求出其横坐标,进而得出菱形ABCD平移的距离.
试题解析:
(1)作DE⊥BO,DF⊥![]() 轴于点F,
轴于点F,
∵点D的坐标为(![]() ,2),
,2),
∴DO= AD=3,
∴A点坐标为:(![]() ,5),
,5),
∴k=![]() ;
;
(2)∵将菱形ABCD向右平移,使点D落在反比例函数![]() (x>0)的图象上D′,
(x>0)的图象上D′,
∴DF=D′F′= 2,
∴D′点的纵坐标为2,
设点D′(![]() , 2)
, 2)
∴![]() ,解得
,解得![]() ,
,
∴![]() ,
,
∴菱形ABCD平移的距离为![]() .
.
同理,将菱形ABCD向右平移,使点B落在反比例函数![]() (x>0)的图象上
(x>0)的图象上
菱形ABCD平移的距离为![]()
综上,当菱形ABCD平移的距离为![]() 或
或![]() 时,菱形的一个顶点恰好落在函数图像上.
时,菱形的一个顶点恰好落在函数图像上.


科目:初中数学 来源: 题型:
【题目】观察下列等式:
第一个等式:a1=![]() =
=![]() -
-![]()
第二个等式:a2= =
=![]() -
-![]()
第三个等式:a3= =
=![]() -
-![]()
第四个等式:a4= =
=![]() -
-![]()
按上述规律,回答下列问题:
(1)请写出第六个等式:a6=_____=_____;
(2)用含n的代数式表示第n个等式:an=_____=_____;
(3)a1+a2+a3+a4+a5+a6=_____(得出最简结果);
(4)计算:a1+a2+…+an.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列解答中,填写适当的理由或数学式:

(1)∵ ∠ABD=∠CDB, ( 已知 )
∴ ∥ . ( )
(2)∵ ∠ADC+∠DCB=180°, ( 已知 )
∴ ∥ . ( )
(3)∵ AD∥BE, ( 已知 )
∴ ∠DCE=∠ . ( )
(4)∵ ∥ , ( 已知 )
∴ ∠BAE=∠CFE. ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为统筹安排大课间体育活动,在各班随机选取了一部分学生,分成四类活动:“篮球”、“羽毛球”、“乒乓球”、“其他”进行调查,整理收集到的数据,绘制成如下的两幅统计图. 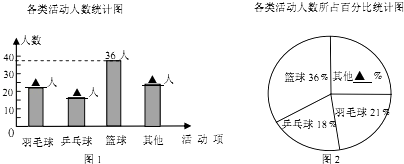
(1)学校采用的调查方式是;学校共选取了名学生;
(2)补全统计图中的数据:条形统计图中羽毛球人、乒乓球人、其他人、扇形统计图中其他%;
(3)该校共有1100名学生,请估计喜欢“篮球”的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com