
【题目】综合与实践
(1)(探索发现)
在△ABC中,AC=BC,∠ACB=a,点D为直线BC上一动点(点D不与点B,C重合),过点D作DF∥AC交直线AB于点F,将AD绕点D顺时针旋转a得到ED,连接BE,如图(1),当点D在线段BC上,且a=90°时,试猜想:
①AF与BE之间的数量关系: ;
②∠ABE= .
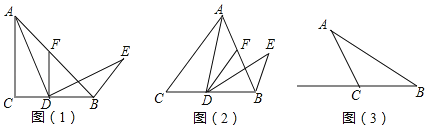
(2)(拓展探究)
如图(2),当点D在线段BC上,且0°<a<90°时,判断AF与BE之间的数量关系及∠ABE的度数,请说明理由.
(3)(解决问题)
如图(3),在△ABC中,AC=BC,AB=4,∠ACB=a,点D在射线BC上,将AD绕点D顺时针旋转a得到ED,连接BE.当BD=3CD时,请直接写出BE的长.
【答案】(1)AF=BF,90°.(2)结论:AF=BE,∠ABE=α.(3)2或4.
【解析】
(1)设AB交DE于O,易证△ADF≌△EDB,得到AF=BE,有因∠DAF=∠E,∠AOD=∠EOB,所以∠ABE=∠ADO=90°
(2)易证△ADF≌△EDB,得到AF=BE,∠AFD=∠EBD,又∠AFD=∠ABC+∠FDB,∠DBE=∠ABD+∠ABE,所以∠ABE=∠FDB=α.
(3)D有可能在BC上,也有可能在BC延长线上,画出图形,利用平行线得到相似,直接利用相似比进行计算即可
解(1)如图1中,设AB交DE于O.

∵∠ACB=90°,AC=BC,
∴∠ABC=45°,
∵DF∥AC,
∴∠FDB=∠C=90°,
∴∠DFB=∠DBF=45°,
∴DF=DB,
∵∠ADE=∠FDB=90°,
∴∠ADF=∠EDB,∵DA=DE,
∴△ADF≌△EDB,
∴AF=BE,∴∠DAF=∠E,
∵∠AOD=∠EOB,
∴∠ABE=∠ADO=90°
故答案为AF=BF,90°.
(2)结论:AF=BE,∠ABE=α.理由如下:
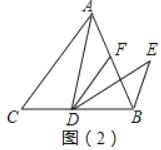
∵DF∥AC
∴∠ACB=∠FDB=α,∠CAB=∠DFB,
∵AC=BC,
∴∠ABC=∠CAB,
∴∠ABC=∠DFB,
∴DB=DF,
∵∠ADF=∠ADE﹣∠FDE,∠EDB=∠FDB﹣∠FDE,
∴∠ADF=∠EDB,
又∵AD=DE,
∴△ADF≌△EDB,
∴AF=BE,∠AFD=∠EBD
∵∠AFD=∠ABC+∠FDB,∠DBE=∠ABD+∠ABE,
∴∠ABE=∠FDB=α.
(3)①如图3﹣1中,当点D在BC上时,
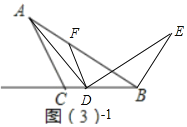
由(2)可知:BE=AF,
∵DF∥AC,
∴![]()
∵AB=8,
∴AF=2,
∴BE=AF=2,
②如图3﹣2中,当点D在BC的延长线上时,
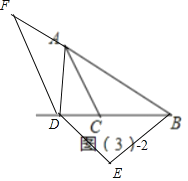
∵AC∥DF,
∴![]()
∵AB=8,
∴AF=4,
故答案为2或4.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】按要求作图,不要求写作法,但要保留作图痕迹.
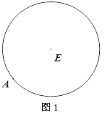
(1)如图1,A为圆E上一点,请用直尺(不带刻度)和圆规作出圆内接正方形;
(2)我们知道,三角形具有性质,三边的垂直平分线相交于同一点,三条角平分线相交于一点,三条中线相交于一点,事实上,三角形还具有性质:三条高交于同一点,请运用上述性质,只用直尺(不带刻度)作图:
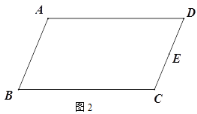
①如图2,在□ABCD中,E为CD的中点,作BC的中点F;
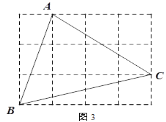
②图3,在由小正方形组成的网格中,的顶点都在小正方形的顶点上,作△ABC的高AH
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,其部分图象如图所示则下列结论:①4a﹣b=0;②c<0;③c>3a;④4a﹣2b>at2+bt(t为实数);⑤点(﹣![]() ,y1),(﹣
,y1),(﹣![]() ,y2),(
,y2),(![]() )是该抛物线上的点,则y2<y1<y3,其中,正确结论的个数是( )
)是该抛物线上的点,则y2<y1<y3,其中,正确结论的个数是( )
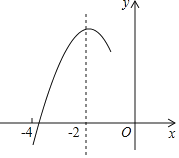
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】称重五筐水果的质量,若每筐以50千克为基准,超过基准部分的千克数记为正数,不足基准部分的千克数记为负数,甲组为实际称重读数,乙组为记录数据,并把所得数据整理成如下统计表和未完成的统计图(单位:千克)
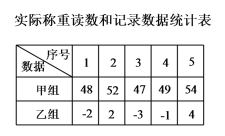
实际称量读数折线统计图 记录数据折线统计图
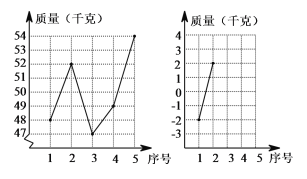
⑴补充完整乙组数据的折线统计图;
⑵①甲、乙两组数据的平均数分别为![]() 、
、![]() ,写出
,写出![]() 与
与![]() 之间的等量关系;
之间的等量关系;
②甲、乙两组数据的平均数分别为![]() 、
、![]() ,比较
,比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
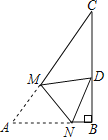
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2![]() +4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.
+4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.玩游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调査,得到如图表(部分信息未给出):
选项 | 频数 | 百分比 |
A | 10 | m |
B | n | 0.2 |
C | 5 | 0.1 |
D | p | 0.4 |
E | 5 | 0.1 |
根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图;
(3)若该中学约有2400名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调査结果,就中学生如何合理使用手机给出你的一条建议.

查看答案和解析>>
科目:初中数学 来源: 题型:
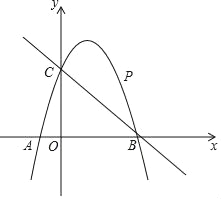
【题目】如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点.
(1)求二次函数y=ax2+2x+c的表达式;
(2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POP′C.若四边形POP′C为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设抛物线 y =m x2 -2m x+3 (m ≠0) 与 x 轴交于点 A (a, 0) 和 B (b, 0) .
(1)若 a =-1,求 m, b 的值;
(2)若 2m +n =3 ,求证:抛物线的顶点在直线 y =m x+ n 上;
(3)抛物线上有两点 P (x1, p) 和 Q (x2 , q) ,若 x1 <1 <x2 ,且 x1 +x2 >2 ,试比较 p 与 q 的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是交警在一个路口统计的某个时段来往车辆的车速情况(单位:千米/时)
(1)找出该样本数据的众数和中位数;
(2)计算这些车的平均速度;(结果精确到0.1)
(3)若某车以50.5千米/时的速度经过该路口,能否说该车的速度要比一半以上车的速度快?并说明判断理由.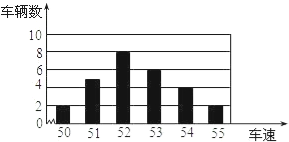
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com