

���� ��1����ͼ��1��������C��CF��y���ڵ�F������ȫ�������Σ���ACF�ա�ABO��AAS������ϸ�ȫ�������εĶ�Ӧ�������OA�ij��ȣ��ɵ�A��y����һ�������֪��A�����ꣻ
��2������C��CG��AC��y���ڵ�G�����ACG�ա�ABD��ASA��������CG=AD=CD����ADB=��G���ɡ�DCE=��GCE=45�㣬��֤��DCE�ա�GCE��SAS���á�CDE=��G���Ӷ��õ����ۣ�
��3��BP�ij��Ȳ��䣬�������£���ͼ��3��������C��CE��y���ڵ�E������ȫ�������Σ���CBE�ա�BAO��AAS�������ȫ�������εĶ�Ӧ�������֪��CE=BO��BE=AO=4���ٽ����֪������ȫ�������ε��ж�����AAS�õ�����CPE�ա�DPB����BP=EP=2��
��� �⣺ ��1����ͼ��1��������C��CF��y���ڵ�F��
��1����ͼ��1��������C��CF��y���ڵ�F��
��CF��y���ڵ�F��
���CFA=90�㣬��ACF+��CAF=90�㣬
�ߡ�CAB=90�㣬
���CAF+��BAO=90�㣬
���ACF=��BAO��
�ڡ�ACF�͡�ABO�У�
$\left\{\begin{array}{l}{��ACF=��BAO}\\{��CFA=��AOB=90��}\\{AC=AB}\end{array}\right.$��
���ACF�ա�ABO��AAS����
��CF=OA=1��
��A��0��1����
��2����ͼ2������C��CG��AC��y���ڵ�G��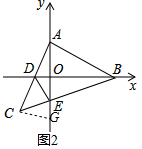 ��CG��AC��
��CG��AC��
���ACG=90�㣬��CAG+��AGC=90�㣬
�ߡ�AOD=90�㣬
���ADO+��DAO=90�㣬
���AGC=��ADO��
�ڡ�ACG�͡�ABD�У�$\left\{\begin{array}{l}{��ACG=��BAD=90��}\\{��AGC=��ADO}\\{AC=AB}\end{array}\right.$��
���ACG�ա�ABD��AAS����
��CG=AD=CD����ADB=��G��
�ߡ�ACB=45�㣬��ACG=90�㣬
���DCE=��GCE=45�㣬
�ڡ�DCE�͡�GCE�У�
$\left\{\begin{array}{l}{CD=CG}\\{��DCE=��GCE}\\{CE=CE}\end{array}\right.$��
���DCE�ա�GCE��SAS����
���CDE=��G��
���ADB=��CDE��
��3��BP�ij��Ȳ��䣬�������£�
��ͼ��3��������C��CE��y���ڵ�E��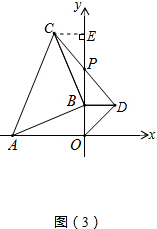
�ߡ�BAC=90�㣬
���CBE+��ABO=90�㣮
�ߡ�BAO+��ABO=90�㣬
���CBE=��BAO��
�ߡ�CEB=��AOB=90�㣬AB=AC��
���CBE�ա�BAO��AAS����
��CE=BO��BE=AO=4��
��BD=BO��
��CE=BD��
�ߡ�CEP=��DBP=90�㣬��CPE=��DPB��
���CPE�ա�DPB��AAS����
��BP=EP=2��
���� ���⿼�����������ۺ��⣮��Ҫ������ȫ�������ε����ʶ������ж��������������Ĺؼ������������ߣ�����ȫ�������Σ�


 �Ƹ�С״Ԫ���ֳ������ϵ�д�
�Ƹ�С״Ԫ���ֳ������ϵ�д� �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д� ����ͬѧһ����ʦȫ�źþ�ϵ�д�
����ͬѧһ����ʦȫ�źþ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����������_����ѧ��մ�������գ���Ϊ����ͼ���ڡ�ABC�У���B=60�㣬AB=6$\sqrt{3}$��tanC=
����������_����ѧ��մ�������գ���Ϊ����ͼ���ڡ�ABC�У���B=60�㣬AB=6$\sqrt{3}$��tanC= ����BC�ij��ȡ������������𰸺�֪BC=6+3$\sqrt{3}$��
����BC�ij��ȡ������������𰸺�֪BC=6+3$\sqrt{3}$�� ����Ϊ$\frac{3}{2}$��
����Ϊ$\frac{3}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
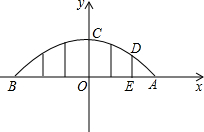 �����߹���y��Գƣ�����C����Ϊ��0��9������x���ڵ�A��d��0����B��-d��0����d��0������ͼ��ABC��Ϊ�������ι��ţ�������˾���ֱ��x�ᣬ�����������߶�AB��6�ȷֵ��ϣ�h=9m��������DE�ij��ȣ�
�����߹���y��Գƣ�����C����Ϊ��0��9������x���ڵ�A��d��0����B��-d��0����d��0������ͼ��ABC��Ϊ�������ι��ţ�������˾���ֱ��x�ᣬ�����������߶�AB��6�ȷֵ��ϣ�h=9m��������DE�ij��ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com