
【题目】已知:二次函数![]() (a为常数).
(a为常数).
(1)请写出该二次函数图象的三条性质;
(2)在同一直角坐标系中,若该二次函数的图象在![]() 的部分与一次函数
的部分与一次函数![]() 的图象有两个交点,求
的图象有两个交点,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)可从开口方向、对称轴、最值等角度来研究即可;
(2) 先由二次函数的图象与一次函数![]() 的图象有两个交点,即关于x的一元二次方程
的图象有两个交点,即关于x的一元二次方程![]() 有两个不相等的实数根,由此可得
有两个不相等的实数根,由此可得![]() ,再根据二次函数的图象在
,再根据二次函数的图象在![]() 的部分与一次函数
的部分与一次函数![]() 的图象有两个交点,也就是说二次函数
的图象有两个交点,也就是说二次函数![]() 的图象与
的图象与![]() 轴
轴![]() 的部分有两个交点,画出函数
的部分有两个交点,画出函数![]() 的图象,结合图象,可知当
的图象,结合图象,可知当![]() 时,
时,![]() ,将x=4代入求得a的取值范围,由此即可求得答案.
,将x=4代入求得a的取值范围,由此即可求得答案.
(1)①图象开口向上;②图象的对称轴为直线![]() ;③当
;③当![]() 时,
时,![]() 随
随![]() 的增大而增大;④当
的增大而增大;④当![]() 时,
时,![]() 随
随![]() 的增大而减小;⑤当
的增大而减小;⑤当![]() 时,函数有最小值;
时,函数有最小值;
(2)∵二次函数的图象与一次函数![]() 的图象有两个交点,
的图象有两个交点,
∴![]() ,即
,即![]() ,
,
![]() ,解得
,解得![]() ,
,
∵二次函数的图象在![]() 的部分与一次函数
的部分与一次函数![]() 的图象有两个交点,
的图象有两个交点,
∴二次函数![]() 的图象与
的图象与![]() 轴
轴![]() 的部分有两个交点,
的部分有两个交点,
画出二次函数![]() 的图象,结合图象,
的图象,结合图象,
可知当![]() 时,
时,![]() ,
,

∴当![]() 时,
时,![]() ,得
,得![]() ,
,
∴当二次函数的图象在![]() 的部分与一次函数
的部分与一次函数![]() 的图象有两个交点时,
的图象有两个交点时,
![]() 的取值范围为
的取值范围为![]() .
.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】现有A、B两个不透明袋子,分别装有3个除颜色外完全相同的小球。其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球。
(1)将A袋摇匀,然后从A袋中随机取出一个小球,求摸出小球是白色的概率;
(2)小华和小林商定了一个游戏规则:从摇匀后的A,B两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜。请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平。
查看答案和解析>>
科目:初中数学 来源: 题型:
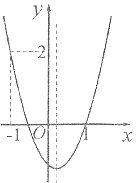
【题目】如图,二次函数![]() 的图象开口向上,图象经过点(-1,2)和(1,0),且与
的图象开口向上,图象经过点(-1,2)和(1,0),且与![]() 轴相交于负半轴,下列结论:①
轴相交于负半轴,下列结论:①![]() ;②方程
;②方程![]() 的两根一个大于1,另一个小于-1;③
的两根一个大于1,另一个小于-1;③![]() ;④
;④![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
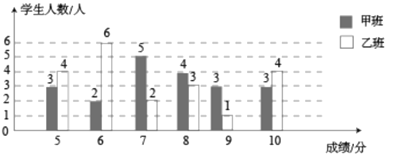
【题目】中华人民共和国第二届青年运动会(简称二青会)将于2019年8月在山西举行,太原市作为主赛区,将承担多项赛事,现正从某高校的甲、乙两班分别招募10人作为颁奖礼仪志愿者,同学们踊跃报名,甲、乙两班各报了20人,现已对他们进行了基本素质测评,满分10分.各班按测评成绩从高分到低分顺序各录用10人,对这次基本素质测评中甲、乙两班学生的成绩绘制了如图所示的统计图.
请解答下列问题:
(1)甲班的小华和乙班的小丽基本素质测评成绩都为7分,请你分别判断小华,小丽能否被录用(只写判断结果,不必写理由).
(2)请你对甲、乙两班各被录用的10名志愿者的成绩作出评价(从“众数”,“中位数”,或“平均数”中的一个方面评价即可).
(3)甲、乙两班被录用的每一位志愿者都将通过抽取卡片的方式决定去以下四个场馆中的两个场馆进行颁奖礼仪服务,四个场馆分别为:太原学院足球场,太原市沙滩排球场,山西省射击射箭训练基地,太原水上运动中心,这四个场馆分别用字母A,B,C,D的四张卡片(除字母外,其余都相同)背面朝上,洗匀放好.志愿者小玲从中随机抽取一张(不放回),再从中随机抽取一张,请你用列表或画树状图的方法求小玲抽到的两张卡片恰好是“A”和“B”的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
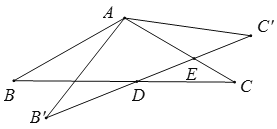
【题目】如图,△ABC中,AB=AC=2,∠B=30°,△ABC绕点A逆时针旋转α(0<α<120°)得到![]() ,
,![]() 与BC,AC分别交于点D,E.设
与BC,AC分别交于点D,E.设![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的函数图象大致为( )
的函数图象大致为( )
A.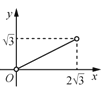 B.
B.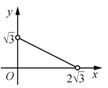 C.
C.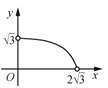 D.
D.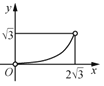
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴相交于点
轴相交于点![]() 、
、![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
![]() 求该函数的表达式;
求该函数的表达式;
![]() 点
点![]() 为该函数在第一象限内的图象上一点,过点
为该函数在第一象限内的图象上一点,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() .
.
①求线段![]() 的最大值;
的最大值;
②若以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
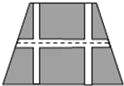
【题目】如图,要设计一个等腰梯形的花坛,花坛上底长120米,下底长180米,上下底相距80米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为x米.
(1)用含x的式子表示横向甬道的面积;
(2)根据设计的要求,甬道的宽不能超过6米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是5.7,花坛其余部分的绿化费用为每平方米0.02万元,那么当甬道的宽度为多少米时,所建花坛的总费用为239万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃停止加热,水温开始下降,此时水温![]() (℃)与开机后用时
(℃)与开机后用时![]() (
(![]() )成反比例关系,直至水温降至30℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时接通电源,水温
)成反比例关系,直至水温降至30℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时接通电源,水温![]() (℃)与时间
(℃)与时间![]() (
(![]() )的关系如图所示:
)的关系如图所示:
(1)分别写出水温上升和下降阶段![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)怡萱同学想喝高于50℃的水,请问她最多需要等待多长时间?

查看答案和解析>>
科目:初中数学 来源: 题型:
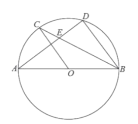
【题目】如图,![]() 为⊙
为⊙![]() 的直径,
的直径,![]() ,
,![]() 为圆上的两点,
为圆上的两点,![]() ,弦
,弦![]() ,
,![]() 相交于点
相交于点![]() ,
,
(1)求证:![]()
(2)若![]() ,
,![]() ,求⊙
,求⊙![]() 的半径;
的半径;
(3)在(2)的条件下,过点![]() 作⊙
作⊙![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 交⊙
交⊙![]() 于
于![]() ,
, ![]() 两点(点
两点(点![]() 在线段
在线段![]() 上),求
上),求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com