
【题目】如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
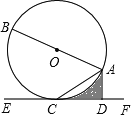
(1)求证:EF是⊙O的切线;
(2)求证:AC2=AD·AB;
(3)若⊙O的半径为2,∠ACD=300,求图中阴影部分的面积.
【答案】解:(1)证明:连接OC,

∵OA=OC,∴∠BAC=∠OCA。
∵∠DAC=∠BAC,∴∠OCA=∠DAC。∴OC∥AD。
∵AD⊥EF,∴OC⊥EF。
∵OC为半径,∴EF是⊙O的切线。
(2)证明:∵AB为⊙O直径,AD⊥EF,
∴∠BCA=∠ADC=90°。
∵∠DAC=∠BAC,∴△ACB∽△ADC。
∴![]() 。∴AC2=ADAB。
。∴AC2=ADAB。
(3)∵∠ACD=30°,∠OCD=90°,∴∠OCA=60°.
∵OC=OA,∴△OAC是等边三角形。∴AC=OA=OC=2,∠AOC=60°。
∵在Rt△ACD中,AD=![]() AC=1。
AC=1。
由勾股定理得:DC=![]() ,
,
∴阴影部分的面积是S=S梯形OCDA﹣S扇形OCA=![]() ×(2+1)×
×(2+1)×![]() ﹣
﹣![]() 。
。
【解析】
试题(1)连接OC,根据OA=OC推出∠BAC=∠OCA=∠DAC,推出OC∥AD,得出OC⊥EF,根据切线的判定推出即可。
(2)证△ADC∽△ACB,得出比例式,即可推出答案。
(3)求出等边三角形OAC,求出AC、∠AOC,在Rt△ACD中,求出AD、CD,求出梯形OCDA和扇形OCA的面积,相减即可得出答案。


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】如图,某公司要建一个矩形的产品展示台,展示台的一边靠找为9m的宣传版(这条边不能超出宣传版),另三边用总长为40m的红布粘贴在展示台边上.设垂直于宣传版的一边长为![]()
(1)当展示台的面积为128m2时,求![]() 的值;
的值;
(2)设展示台的面积为![]() ,求
,求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+(m﹣1)x+m的对称轴为x=![]() ,请你解答下列问题:
,请你解答下列问题:
(1)m= ,抛物线与x轴的交点为 .
(2)x取什么值时,y的值随x的增大而减小?
(3)x取什么值时,y<0?
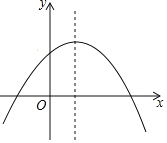
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O直径,半径OC⊥AB,连接AC,∠CAB的平分线AD分别交OC于点E,交![]() 于点D,连接CD、OD,以下三个结论:①AC∥OD;②AC=2CD;③线段CD是CE与CO的比例中项,其中所有正确结论的序号是( )
于点D,连接CD、OD,以下三个结论:①AC∥OD;②AC=2CD;③线段CD是CE与CO的比例中项,其中所有正确结论的序号是( )

A.①②B.②③
C.①③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
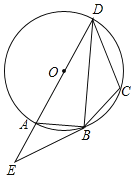
【题目】如图,四边形ABCD的外接圆为⊙O,AD是⊙O的直径,过点B作⊙O的切线,交DA的延长线于点E,连接BD,且∠E=∠DBC.
(1)求证:DB平分∠ADC;
(2)若CD=9,tan∠ABE=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形![]() 的两个顶点
的两个顶点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图象上,对角线
的图象上,对角线![]() 与
与![]() 的交点恰好是坐标原点
的交点恰好是坐标原点![]() ,已知点
,已知点![]() ,
,![]() .
.

(1)求反比例函数的解析式;
(2)点![]() 是
是![]() 轴上一点,若
轴上一点,若![]() 是等腰三角形,直接写出点
是等腰三角形,直接写出点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我们可以将x2﹣1视为一个整体,然后设x2﹣1=y,则
(x2﹣1)=y2,原方程化为y2﹣5y+4=0.①
解得y1=1,y2=4
当y=1时,x2﹣1=1.∴x2=2.∴x=±![]() ;
;
当y=4时,x2﹣1=4,∴x2=5,∴x=±![]() .
.
∴原方程的解为x1=![]() ,x2=﹣
,x2=﹣![]() ,x3=
,x3=![]() ,x4=﹣
,x4=﹣![]()
解答问题:
(1)填空:在由原方程得到方程①的过程中,利用 法达到了降次的目的,体现了 的数学思想.
(2)解方程:x4﹣x2﹣6=0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com