
分析 (1)通过理解题意可知本题的等量关系,即甲单独修完这些桌凳的天数=乙单独修完的天数+20天,列方程求解即可;
(2)分别求出三种方案的总费用,比较后即可得.
解答 解:(1)设该中学库存x套桌椅,
则甲需要$\frac{x}{16}$天,乙需要$\frac{x}{16+8}$天,
根据题意得:$\frac{x}{16}$-$\frac{x}{16+8}$=20,
解得:x=960,
答:该中学库存960套桌椅;
(2)方案a的费用为(80+10)×$\frac{960}{16}$=5400(元),
方案b的费用为(120+10)×$\frac{960}{16+8}$=5200(元),
方案c的费用为(80+120+10)×$\frac{960}{16+16+8}$=5040(元),
综上,方案c的费用省时又省力.
点评 本题考查了一元一次方程的应用,解题的关键是找到等量关系:甲单独修完这些桌凳的天数=乙单独修完的天数+20天.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
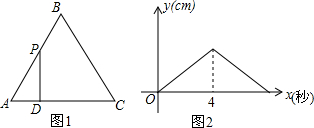
| A. | $\frac{5\sqrt{3}}{4}$cm | B. | $\frac{5\sqrt{3}}{2}$cm | C. | 2$\sqrt{3}$cm | D. | 3$\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
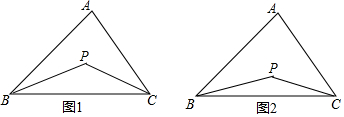 【提出问题】已知如图1,P是∠ABC、∠ACB的角平分线的交点,你能找到∠P、∠A的关系吗?
【提出问题】已知如图1,P是∠ABC、∠ACB的角平分线的交点,你能找到∠P、∠A的关系吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
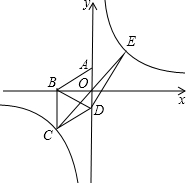 如图,在平面直角坐标系中四边形ABCD为菱形,边AD在y轴上.其中A(0,1),B(-$\sqrt{3}$,0),双曲线y=$\frac{m}{x}$经过点C.
如图,在平面直角坐标系中四边形ABCD为菱形,边AD在y轴上.其中A(0,1),B(-$\sqrt{3}$,0),双曲线y=$\frac{m}{x}$经过点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com