
【题目】如图,已知△ABE与△CDE都是等腰直角三角形,∠AEB=∠DEC=90°,连接AD,AC,BC,BD,若AD=AC=AB,则下列结论:①AE垂直平分CD,②AC平分∠BAD,③△ABD是等边三角形,④∠BCD的度数为150°,其中正确的个数是( )

A.1B.2C.3D.4
【答案】D
【解析】
首先证明△AEC≌△BED,得到AC=BD=AB=AD,得到△ABD是等边三角形,③正确;根据 ABE与 CDE都是等腰直角三角形,得到∠CAB=∠CAD=30°∠CAE=∠EAD=15°得到①②正确; ABC,CAD为等腰三角形,顶角都为30°,得到∠ACB=∠ABC=75°,∠ACD=∠ADC=75°,得出∠BCD的度数为150°④正确
解:∵ ABE与 CDE都是等腰直角三角形
∴AE=BE, DE=CE
∵∠AEB=∠DEC=90°
∴∠AEC=∠DEB
∴△AEC≌△BED
∴AC=BD
∵AD=AC=AB
∴AD=BD=AB
∴② ABD是等边三角形正确
∴∠ABD=∠BAD=∠ADB=60°
∵ ABE与 CDE都是等腰直角三角形
∴∠EAB=∠ABE=45°
∴∠CAB=30°,∠CAE=∠EAD=15°
∴AE为∠CAD的角平分线
∵ ABD为等腰三角形
∴①AE垂直平分CD正确
∴∠CAD=30°
∴②AC平分∠BAD正确
∵ ABC为等腰三角形,顶角∠BAC=30°
∴∠ACB=∠ABC=75°
同理∠ACD=∠ADC=75°
∴④∠BCD的度数为150°正确.
故选D


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】如图,分别以直角三角形的三边为边长向外作正方形,然后分别以三个正方形的中心为圆心,正方形边长的一半为半径作圆,记三个圆的面积分别为![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() 之间的关系是( )
之间的关系是( )

A.![]() B.
B.![]() C.
C.![]() D.无法确定
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组进行户外兴趣活动:测量河中桥墩露出水面部分AB的高度.如图所示,在点C处测得∠BCA=45°.在坡比为i=1:3,高度DE=15米的小山坡顶E处测得桥墩顶部B的仰角为20°,则桥墩露出水面部分AB的高度约为(精确到1米,参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)( )

A. 34 B. 48 C. 49 D. 64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为使中华传统文化教育更具有实效性,军宁中学开展以“我最喜爱的传统文化种类”为主题的调查活动,围绕“在诗词、国画、对联、书法、戏曲五种传统文化中,你最喜爱哪一种?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:
(1)本次调查共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)若军宁中学共有960名学生,请你估计该中学最喜爱国画的学生有多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夷陵区园林处为了对一段公路进行绿化,计划购买A、B两种风景树,已知若用8000元买A种树要比买B种树多买20棵,A、B两种树的相关信息如下表:
项目品种 | 单价(元/棵) | 成活率 |
A | m | 91% |
B | 100 | 97% |
(1)求表中m的值;
(2)预计对这段公路的绿化需购1000棵这样的风景树.若希望这批树的成活率不低于94%,且使购树的总费用最低,应选购A、B两种树各多少棵?最低费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从A地到B地的公路需要经过C地,根据规划,将在A,B两地之间修建一条笔直的公路.已知AC=10千米,∠CAB=34°,∠CBA=45°,求改直后公路AB的长(结果精确到0.1千米)
(参考数据:sin34°≈0.559,cos34°≈0.829,tan34°≈0.675)

查看答案和解析>>
科目:初中数学 来源: 题型:
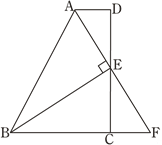
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F. 已知AD=2cm,BC=5cm.
(1)求证:FC=AD;
(2)求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣2x+m的图象与x轴y轴分别交于点A,B,与正比例函数y=![]() x的图象交于点P(2,n)
x的图象交于点P(2,n)
(1)求点A的坐标;
(2)求△POB的面积.
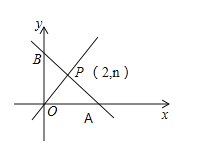
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com