Question

10．如图1，在△ABC中，AB=AC，BC=12，D、E是AB、AC上的点，DE∥BC，BD=5，DE=6，P是线段DE上一点，PE=2DP，N是线段BD上一点，MN∥CP交BC于点M．
（1）求AB和cosB；
（2）如图2，设BN=x，CM=y，试用含x的式子表示y；
（3）连PM，若△PMC为直角三角形，则x=$\frac{5}{2}$或$\frac{19}{14}$．

Answer 1

分析 （1）如图1中，作DM⊥BC于M，EN⊥BC于N．由DE∥BC，得$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{6}{12}$=$\frac{1}{2}$，可以解决AB，再证明△DMB≌△ENC，求出BM，即可解决问题．
（2）如图2中，作DH∥MN交BC于H．先证明四边形DPCH是平行四边形，由MN∥DH，得$\frac{BN}{BD}$=$\frac{BM}{BH}$，列出等式，即可解决问题．
（3）分两种情形讨论①当∠PMC=90°时，作EG⊥BC于G．当∠MPC=90°时，作PH⊥BC于H，EG⊥BC于G，分别求解即可．

解答 解：（1）如图1中，作DM⊥BC于M，EN⊥BC于N．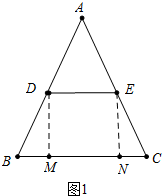

∵DE∥BC，
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{6}{12}$=$\frac{1}{2}$，
∵BD=5，
∴AD=BD=5，AB=2AD=10．
∵DM∥EN，DE∥MN，
∴四边形DENM是平行四边形，
∵∠DMN=90°，
∴四边形DENM是矩形，
∴DE=MN=6，DM=EN，
∵AB=AC，
∴∠B=∠C，
在△DMB和△ENC中，
$\left\{\begin{array}{l}{∠DMB=∠ENC}\\{∠B=∠C}\\{DM=EN}\end{array}\right.$，
∴△DMB≌△ENC，
∴BM=CN=3，
在Rt△DBM中，∵cos∠B=$\frac{BM}{BD}$
∴cos∠B=$\frac{3}{5}$．

（2）如图2中，作DH∥MN交BC于H．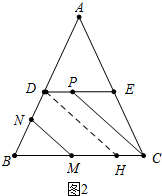

∵MN∥CP，DH∥NM，
∴DH∥PC，∵DP∥CH，
∴四边形DPCH是平行四边形，
∵DE=6，PE=2DP，
∴PD=2，PE=4，
∴DP=CH=2，MH=y-2，
∵MN∥DH，
∴$\frac{BN}{BD}$=$\frac{BM}{BH}$，
∴$\frac{x}{5}$=$\frac{12-y}{10}$，
∴y=12-2x．（0≤x≤5）

（3）①当∠PMC=90°时，如图3中，作EG⊥BC于G．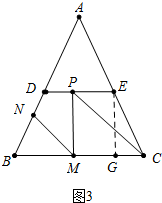

由（1）可知，CG=3，PE=MG=4，
在Rt△PCM中，∵∠PMC=90°，PM=4，CM=7，
∴y=7，
∴7=12-2x，
∴x=$\frac{5}{2}$．
②当∠MPC=90°时，如图4中，作PH⊥BC于H，EG⊥BC于G，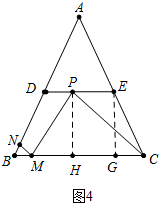

∵∠MPH+∠CPH=90°，∠CPH+∠PCH=90°，
∴∠MPH=∠PCH，
∵∠PHM=∠PHC=90°，
∴△PHM∽△CHP，
∴$\frac{PH}{CH}$=$\frac{HM}{HP}$，
∴$\frac{4}{7}$=$\frac{HM}{4}$，
∴HM=$\frac{16}{7}$，
∴y=CM=$\frac{16}{7}$+7=$\frac{65}{7}$，
∴$\frac{65}{7}$=12-2x，
∴x=$\frac{19}{14}$．
综上所述，△PMC为直角三角形时，x=$\frac{5}{2}$或$\frac{19}{14}$．
故答案为$\frac{5}{2}$或$\frac{19}{14}$．

点评 本题考查三角形综合题、平行线分线段成比例定理、相似三角形的判定和性质．全等三角形的判定和性质等知识，解题的关键是重合添加常用辅助线构造全等三角形解决问题，学会分类讨论的思想，注意考虑问题要全面，属于中考压轴题．