
 若P、Q是线段AB上的两个黄金分割点,且PQ=2$\sqrt{5}$-4,则AB=2.
若P、Q是线段AB上的两个黄金分割点,且PQ=2$\sqrt{5}$-4,则AB=2. 分析 设AB=x,根据P、Q是线段AB上的两个黄金分割点,用x表示出AQ和AP的长,根据题意列出方程,解方程得到答案.
解答 解:设AB=x,
∵P、Q是线段AB上的两个黄金分割点,
∴AQ=BP=$\frac{\sqrt{5}-1}{2}$x,
AP=AB-BQ=x-$\frac{\sqrt{5}-1}{2}$x=$\frac{3-\sqrt{5}}{2}$x,
∵PQ=AQ-AP,
∴$\frac{\sqrt{5}-1}{2}$x-$\frac{3-\sqrt{5}}{2}$x=2$\sqrt{5}$-4,
解得,x=2,
故答案为:2.
点评 本题考查度数黄金分割的知识,黄金分割的概念:把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,较长的线段与全线段的比值$\frac{\sqrt{5}-1}{2}$叫做黄金比.


科目:初中数学 来源: 题型:填空题
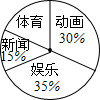 某校调查了九年级820名学生对新闻、体育、动画、娱乐四类电视节目的喜爱情况,绘制成所示的扇形统计图,则该校喜爱体育节目的学生有164名.
某校调查了九年级820名学生对新闻、体育、动画、娱乐四类电视节目的喜爱情况,绘制成所示的扇形统计图,则该校喜爱体育节目的学生有164名.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 菱形ABCD的边长为1,∠C=60°,E、F分别在BC、CD上,且EF⊥CD,则△AEF面积的最大值为$\frac{\sqrt{3}}{4}$.
菱形ABCD的边长为1,∠C=60°,E、F分别在BC、CD上,且EF⊥CD,则△AEF面积的最大值为$\frac{\sqrt{3}}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com