
 如图,已知正方形ABCD,AB=4,动点M、N分别从D、B两点同时出发,且都以1个单位/秒的速度匀速运动,点M沿DA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥AD,交AC于点P,连结NP.设运动时间为x秒.
如图,已知正方形ABCD,AB=4,动点M、N分别从D、B两点同时出发,且都以1个单位/秒的速度匀速运动,点M沿DA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥AD,交AC于点P,连结NP.设运动时间为x秒.分析 (1)由题意知MD=x,则AM=4-x,根据正方形的性质得到CD⊥AD,根据相似三角形的性质得到$\frac{AM}{AD}=\frac{PM}{CD}$,代入数据即可得到结论;
(2)如图1,延长MP交BC于Q点,根据正方形的性质得到∠D=∠BCD=90°,AB=BC=CD=4,推出四边形MQCD是矩形,根据矩形的性质得到∠PQC=90°,MQ=CD,根据三角形的面积公式即可得到结论;
(3)当CN=PN时 如图2,由正方形的性质得到∠NCP=45°,得到∠PNC=90°,求得x=2,当CN=CP时,如图3,CN=4-x,CQ=MD=x根据等腰直角三角形得到CP=$\sqrt{2}$CQ=$\sqrt{2}x$,于是得到x=4$\sqrt{2}$-4,当PN=CP时,如图4,求得∠NPC=90°,根据直角三角形的性质得到$x=\frac{4}{3}$.
解答 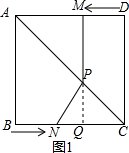 解:(1)由题意知:MD=x,则AM=4-x,
解:(1)由题意知:MD=x,则AM=4-x,
∵四边形ABCD正方形,
∴CD⊥AD,
∵MP⊥AD,
∴MP∥CD,
∴△AMP∽△ADC,
∴$\frac{AM}{AD}=\frac{PM}{CD}$,
∴$\frac{4-x}{4}=\frac{PM}{4}$,
∴PM=4-x,
故答案为:4-x;
(2)如图1,延长MP交BC于Q点,
∵四边形ABCD是正方形,
∴∠D=∠BCD=90°,AB=BC=CD=4,
∵MP⊥AD,
∴∠PMD=90°,
∴四边形MQCD是矩形,
∴∠PQC=90°,MQ=CD,
∴PQ⊥NC,
∵CD=4,
∴MQ=4,
由(1)知MP=4-x,
∴PQ=x,
据题意得 BN=x,
∴CN=4-x,
∴S=$\frac{1}{2}$NC•PQ=$\frac{1}{2}$x(4-x)=2x-$\frac{1}{2}$x2(0<x<4);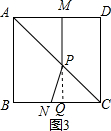
(3)当CN=PN时 如图2,
∴∠NPC=∠NCP,
∵四边形ABCD是正方形,
∴∠NCP=45°,
∴∠PNC=90°,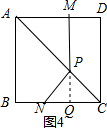
CN=4-x,PN=x,
∴x=2,
当CN=CP时,如图3,CN=4-x,CQ=MD=x
等腰直角三角形 PQC中,CP=$\sqrt{2}$CQ=$\sqrt{2}x$,
∴x=4$\sqrt{2}$-4,
当PN=CP时,如图4,
∴∠PNC=∠PCN=45°,
∴∠NPC=90°,
∵PQ⊥NC∴Q是NC的中点,
∴NC=2PQ,
∴$x=\frac{4}{3}$.
点评 本题考查了矩形的性质,正方形的性质,相似三角形的判定和性质,等腰直角三角形的性质,正确的作出辅助线构造直角三角形是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售额/万元 | 29 | 32 | 34 | 38 | 48 | 55 |
| 专卖店/个数 | 1 | 1 | 3 | 2 | 2 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABD中,∠BDA=90°,AD=BD,点E在AD上,连接BE,将△BED绕点D顺时针旋转90°,得到△ACD,若∠BED=65°,则∠ACE的度数为( )
如图,在Rt△ABD中,∠BDA=90°,AD=BD,点E在AD上,连接BE,将△BED绕点D顺时针旋转90°,得到△ACD,若∠BED=65°,则∠ACE的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com