
分析 根据“伴随点”的定义依次求出各点,不难发现,每4个点为一个循环组依次循环,用2015除以4,根据商和余数的情况确定点A2015的坐标即可;再写出点A1(a,b)的“伴随点”,然后根据x轴上方的点的纵坐标大于0列出不等式组求解即可.
解答 解:∵A1的坐标为(4,5),
∴A2(-4,5),A3(-4,-3),A4(4,-3),A5(4,5),
…,
依此类推,每4个点为一个循环组依次循环,
∵2015÷4=503余3,
∴点A2015的坐标与A3的坐标相同,为(-4,-3);
∵点A1的坐标为(a,b),
∴A2(-b+1,a+1),A3(-a,-b+2),A4(b-1,-a+1),A5(a,b),
…,
依此类推,每4个点为一个循环组依次循环,
∵对于任意的正整数n,点An均在x轴上方,
∴$\left\{\begin{array}{l}{a+1>0}\\{-a+1>0}\end{array}\right.$,$\left\{\begin{array}{l}{-b+2>0}\\{b>0}\end{array}\right.$,
解得-1<a<1,0<b<2.
故答案为:(-4,-3);-1<a<1且0<b<2.
点评 本题是对点的变化规律的考查,读懂题目信息,理解“伴随点”的定义并求出每4个点为一个循环组依次循环是解题的关键,也是本题的难点.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
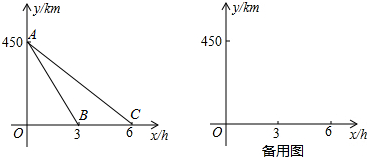
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
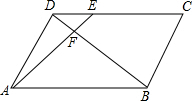 如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD相交于点F,DE:EC=2:3,则S△DEF:S△ABF等于( )
如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD相交于点F,DE:EC=2:3,则S△DEF:S△ABF等于( )| A. | 4:25 | B. | 4:9 | C. | 9:25 | D. | 2:3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
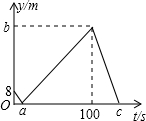 甲、乙两人在一条长为500m的直线跑道上同起点、同向匀速跑步,已知甲先出发2s后乙再出发,先到终点的人原地休息,如图表示的是甲、乙两人之间的距离y(m)与乙出发的时间t(s)的函数关系,给出以下结论:①a=8;②b=92;③c=23,其中正确的是( )
甲、乙两人在一条长为500m的直线跑道上同起点、同向匀速跑步,已知甲先出发2s后乙再出发,先到终点的人原地休息,如图表示的是甲、乙两人之间的距离y(m)与乙出发的时间t(s)的函数关系,给出以下结论:①a=8;②b=92;③c=23,其中正确的是( )| A. | ①②③ | B. | ①② | C. | ①③ | D. | ②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
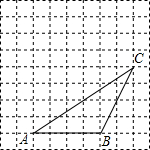 如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度.
如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com