分析:根据过O作OL⊥CG,则△GOL∽△GBC,利用相似三角形的性质即可得出OL的长度,进而求出△DBO的面积.
解答: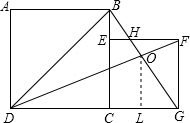
解:过O作OL⊥CG,
∵正方形ABCD的面积为64cm
2,
∴BC=
=8,
∵正方形CEFG的面积为36cm
2,
∴CG=
=6,
∴BG=
=10,
∵BC=8,CE=6,CG=2,BE=BC-CE=8-6=2,
∵EF∥CG,
∴Rt△BEH∽Rt△BCG,
∴
=
=
,
即
=
=
,
∴BH=
,EH=
,
在△DOG与△FOH中,∠DOG=∠FOH,
∵EF∥CG,
∴∠HFO=∠FDC,
∴△DOG∽△FOH,
∴
=
,HF=EF-EH=6-
=
,DC+CG=8+6=14,OG=BG-BH-OH=10-
-OH=
-OH,
故
=
,
∴OH=
,BO=BH+OH=
+
=
.
∵△GOL∽△GBC,
∴OG=BG-BO=10-
=
,
=
=
,
解得OL=
,
∴S
△DBO=S
△BDG-S
△DOG=
DG•BC-
DG•OL,
=
DG×(BC-OL),
=
×14×(8-
),
=7×
,
=
,
=24
.
故答案为:24
.
点评:此题主要考查了相似三角形的判定与性质以及正方形的性质等知识,解答本题要充分利用正方形的特殊性质,注意在正方形中的特殊三角形的应用,及勾股定理的应用.

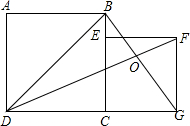 如图所示,正方形ABCD的面积是64cm2,正方形CEFG的面积是36cm2,DF与BG相交于点O,则△DBO的面积等于
如图所示,正方形ABCD的面积是64cm2,正方形CEFG的面积是36cm2,DF与BG相交于点O,则△DBO的面积等于 解:过O作OL⊥CG,
解:过O作OL⊥CG,

 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案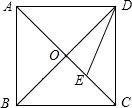 如图所示,正方形ABCD的对角线AC,BD相交于点O,DE平分∠ODC交OC于点E,若AB=2,则线段OE的长为( )
如图所示,正方形ABCD的对角线AC,BD相交于点O,DE平分∠ODC交OC于点E,若AB=2,则线段OE的长为( )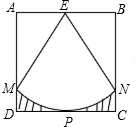 如图所示,正方形ABCD的边长为1,点E为AB的中点,以E为圆心,1为半径作圆,分别交AD,BC于M,N两点,与DC切于点P,则图中阴影部分面积是
如图所示,正方形ABCD的边长为1,点E为AB的中点,以E为圆心,1为半径作圆,分别交AD,BC于M,N两点,与DC切于点P,则图中阴影部分面积是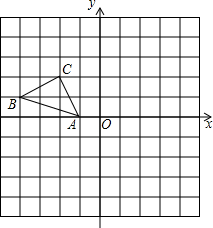 如图所示的正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
如图所示的正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题: