
 为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行),通道水平宽度BC为8米,∠BCD=135°,通道斜面CD的长为6米,通道斜面AB的坡度i=1:$\sqrt{2}$.
为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行),通道水平宽度BC为8米,∠BCD=135°,通道斜面CD的长为6米,通道斜面AB的坡度i=1:$\sqrt{2}$.分析 (1)过点A作AN⊥CB于点N,过点D作DM⊥BC于点M,解Rt△CMD,得出DM=CM=$\frac{\sqrt{2}}{2}$CD=3$\sqrt{2}$,则AN=DM=3$\sqrt{2}$,再解Rt△ANB,由通道斜面AB的坡度i=1:$\sqrt{2}$,得出BN=$\sqrt{2}$AN=6,然后根据勾股定理求出AB;
(2)先解Rt△MED,求出EM=$\sqrt{3}$DM=3$\sqrt{6}$,那么EC=EM-CM=3$\sqrt{6}$-3$\sqrt{2}$,再根据BE=BC-EC即可求解.
解答  解:(1)过点A作AN⊥CB于点N,过点D作DM⊥BC于点M,
解:(1)过点A作AN⊥CB于点N,过点D作DM⊥BC于点M,
∵∠BCD=135°,
∴∠DCM=45°.
∵在Rt△CMD中,∠CMD=90°,CD=6,
∴DM=CM=$\frac{\sqrt{2}}{2}$CD=3$\sqrt{2}$,
∴AN=DM=3$\sqrt{2}$,
∵通道斜面AB的坡度i=1:$\sqrt{2}$,
∴tan∠ABN=$\frac{AN}{BN}$=$\frac{1}{\sqrt{2}}$,
∴BN=$\sqrt{2}$AN=6,
∴AB=$\sqrt{A{N}^{2}+B{N}^{2}}$=3$\sqrt{6}$≈7.4.
即通道斜面AB的长约为7.4米;
(2)∵在Rt△MED中,∠EMD=90°,∠DEM=30°,DM=3$\sqrt{2}$,
∴EM=$\sqrt{3}$DM=3$\sqrt{6}$,
∴EC=EM-CM=3$\sqrt{6}$-3$\sqrt{2}$,
∴BE=BC-EC=8-(3$\sqrt{6}$-3$\sqrt{2}$)=8+3$\sqrt{2}$-3$\sqrt{6}$≈4.9.
即此时BE的长约为4.9米.
点评 本题考查了解直角三角形的应用-坡度坡角问题,三角函数的定义,勾股定理,准确作出辅助线构造直角三角形是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
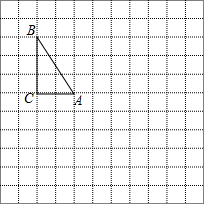 如图是边长为1个单位长度的小正方形组成的网格,在格点△ABC中,∠C=90°,AC=2,BC=3.
如图是边长为1个单位长度的小正方形组成的网格,在格点△ABC中,∠C=90°,AC=2,BC=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,点P在BA的延长线上,过点P作⊙O的切线,切点为D,PD的延长线与弦BE的延长线交于点C,连接BD.
如图,AB是⊙O的直径,点P在BA的延长线上,过点P作⊙O的切线,切点为D,PD的延长线与弦BE的延长线交于点C,连接BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com