
分析 (1)先求得抛物线与x轴两交点的坐标为A(-m,0),B(3m,0).,然后再求得点C的坐标,然后依据△ABC的面积为6列方程求解即可;
(2)过点E作EM⊥x轴,垂足为M,过点D作DN⊥x轴,垂足为N.由题意可知D(a,a2-2ma-3m2),E(b,b2-2mb-3m2),AN=a+m,AM=b+m,ND=-a2+2ma+3m2,ME=b2-2mb-3m2,然后依据∠tanEAN=tan∠DAN可得到a、b、m的关系式,通过变形可得到$\frac{a+b}{m}$的值;
(3)过点E作EM⊥x轴,垂足为M,过点D作DN⊥x轴,垂足为N.先求得抛物线的对称轴方程,则可得到点D的横坐标,由(2)中的结论可求得点E的横坐标为4m,故此可得到AN和AM的长,然后再证明△AEM∽△ADN,依据相似三角形的性质可知$\frac{AE}{AD}$=$\frac{AN}{AM}$,于是可求得$\frac{AE}{AD}$的值.
解答 解:(1)令y=0得:x2-2mx-3m2=0,解得x=-m或x=3m,
∵m>0,点A在点B左侧,
∴A(-m,0),B(3m,0).
当x=0时,y=-3m2,
∴C(0,-3m2).
∵△ABC的面积为6,
∴$\frac{1}{2}$×4m×3m2=6,解得m=1.
∴抛物线的解析式为y=x2-2x-3.
(2)如图1所示:过点E作EM⊥x轴,垂足为M,过点D作DN⊥x轴,垂足为N.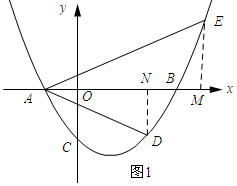
∵点D、E的横坐标分别为a、b,
∴D(a,a2-2ma-3m2),E(b,b2-2mb-3m2).
∴AN=a+m,AM=b+m,ND=-a2+2ma+3m2,ME=b2-2mb-3m2.
∵AB平分∠DAE,
∴∠tanEAN=tan∠DAN.
∴$\frac{EM}{AM}=\frac{DN}{AN}$,即$\frac{{b}^{2}-2mb-3{m}^{2}}{b+m}=\frac{-{a}^{2}+2ma+3{m}^{2}}{a+m}$.
∴b-3m=-(a-3m).
∴a+b=6m.
∴$\frac{a+b}{m}$=6.
(3)过点E作EM⊥x轴,垂足为M,过点D作DN⊥x轴,垂足为N.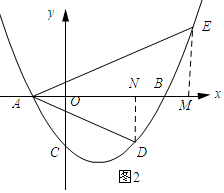
∵x=-$\frac{b}{2a}$,
∴抛物线的对称轴为x=m.
∵CD∥x轴,C(0,-3m2)
∴D(2m,-3m2).
设点E的坐标横坐标为b.
由(2)可知2m+b=6m,解得:b=4m,
∴AN=3m,AM=5m.
∵∠EAM=∠DAN,∠AND=∠AME=90°,
∴△EAM∽△DAN.
∴$\frac{AE}{AD}$=$\frac{AM}{AN}$=$\frac{5m}{3m}$=$\frac{5}{3}$.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了三角形的面积公式、锐角三角函数的定义、相似三角形的性质和判定,用含m的式子表示出AN、AM的长是解答本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
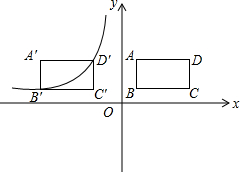 如图所示,在平面直角坐标系中,矩形ABCD,AB=2,BC=4,点B(1,1).
如图所示,在平面直角坐标系中,矩形ABCD,AB=2,BC=4,点B(1,1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
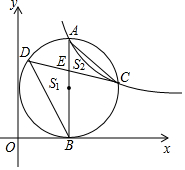 如图,点A是反比例函数y=$\frac{k}{x}$(k>0)图象第一象限上一点,过点A作AB⊥x轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点E.记△BDE的面积为S1,△ACE的面积为S2,若S1-S2的值最大为1,则k的值为4$\sqrt{2}$+4.
如图,点A是反比例函数y=$\frac{k}{x}$(k>0)图象第一象限上一点,过点A作AB⊥x轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点E.记△BDE的面积为S1,△ACE的面积为S2,若S1-S2的值最大为1,则k的值为4$\sqrt{2}$+4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
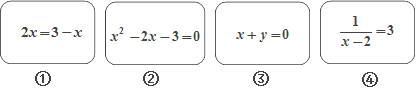
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 应试者 | 听 | 说 | 读 | 写 |
| 甲 | 85 | 78 | 85 | 73 |
| 乙 | 73 | 80 | 82 | 83 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 累计购物 | 130 | 250 | … |
| 在甲商场 实际花费 | 100+(130-100)×90% | 100+(250-100)×90% | … |
| 在乙商场 实际花费 | 50+(130-50)×95% | 50+(250-50)×95% | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
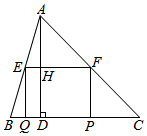 如图,在锐角△ABC中,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.
如图,在锐角△ABC中,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com