
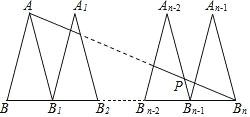
【题目】如图,△ABB1,△A1B1B2,…,△An﹣2Bn﹣2Bn﹣1,△An﹣1Bn﹣1Bn是n个全等的等腰三角形,其中AB=2,BB1=1,底边BB1,B1B2,…,Bn﹣2Bn﹣1,Bn﹣1Bn在同一条直线上,连接ABn交An﹣2Bn﹣1于点P,则PBn﹣1的值为__.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
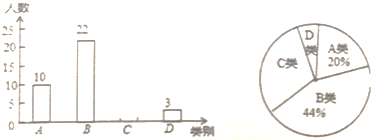
【题目】中华民族,源远流长:中华诗词,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校学生参加的“中国诗词大会”海选比赛,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了部分学生的海选比赛成绩(满分100分,成绩m均为整数分),并按测试成绩(单位:分)分成四类:A类(85≤m≤100),B类(70≤m≤84),C类(60≤m≤69),D类(m≤59)绘制出以下两幅不完整的统计图,请根据图中信息解答下列问题:
(1)求本次抽取的学生人数,并补全条形统计图;
(2)所抽取学生的海选比赛成绩的中位数落在哪类;
(3)若该学校学生有1500名,请估计该学校本次海选比赛成绩为D类的学生人数,并请你给这些学生提出一条与学习诗词有关的合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,如图1,AB是⊙O的弦,点F是![]() 的中点,过点F作EF⊥AB于点E,易得点E是AB的中点,即AE=EB.⊙O上一点C(AC>BC),则折线ACB称为⊙O的一条“折弦”.
的中点,过点F作EF⊥AB于点E,易得点E是AB的中点,即AE=EB.⊙O上一点C(AC>BC),则折线ACB称为⊙O的一条“折弦”.
(1)当点C在弦AB的上方时(如图2),过点F作EF⊥AC于点E,求证:点E是“折弦ACB”的中点,即AE=EC+CB.
(2)当点C在弦AB的下方时(如图3),其他条件不变,则上述结论是否仍然成立?若成立说明理由;若不成立,那么AE、EC、CB满足怎样的数量关系?直接写出,不必证明.
(3)如图4,已知Rt△ABC中,∠C=90°,∠BAC=30°,Rt△ABC的外接圆⊙O的半径为2,过⊙O上一点P作PH⊥AC于点H,交AB于点M,当∠PAB=45°时,求AH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正五边形ABCDE内接于⊙O点F为![]() 的中点,直线AP与⊙O相切于点A,则∠FAP的度数是( )
的中点,直线AP与⊙O相切于点A,则∠FAP的度数是( )
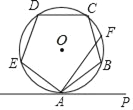
A. 36°B. 54°C. 60°D. 72°
查看答案和解析>>
科目:初中数学 来源: 题型:
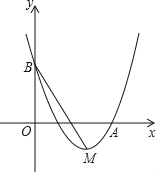
【题目】如图在平面直角坐标系xOy中,O为坐标原点,二次函数y=x2+bx+c的图象经过点A(3,0)、点B(0,3),顶点为M.
(1)求该二次函数的解析式;
(2)求∠OBM的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
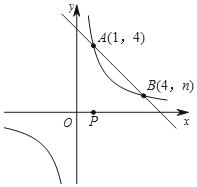
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)直接写出当x>0时,kx+b<![]() 的解集.
的解集.
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师将![]() 个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
摸球的次数 |
|
|
|
|
|
|
摸到黑球的次数 |
|
|
|
|
|
|
摸到黑球的频率 |
|
|
|
|
|
![]() 补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________(精确到0.01);
补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________(精确到0.01);
![]() 估算袋中白球的个数;
估算袋中白球的个数;
![]() 在
在![]() 的条件下,若小强同学有放回地连续两次摸球,用画树状图或列表的方法计算他两次都摸出白球的概率.
的条件下,若小强同学有放回地连续两次摸球,用画树状图或列表的方法计算他两次都摸出白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
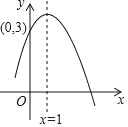
【题目】如图,已知二次函数y=ax2+bx+c的图象经过点(0,3),(x1,0),其中,2<x1<3,对称轴为x=1,则下列结论:①2a﹣b=0; ②x(ax+b)≤a+b;③方程ax2+bx+c﹣3=0的两根为x1'=0,x2'=2;④﹣3<a<﹣1.其中正确的是( )
A. ②③④B. ①②③C. ②④D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明袋子中装有三只大小、质地都相同的小球,球面上分别标有数字1、﹣2、3,搅匀后先从中任意摸出一个小球(不放回),记下数字作为点A的横坐标,再从余下的两个小球中任意摸出一个小球,记下数字作为点A的纵坐标.
(1)用画树状图或列表等方法列出所有可能出现的结果;
(2)求点A落在第四象限的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com