
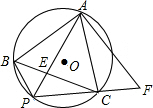
 如图,正三角形ABC内接于⊙O,P是BC上的一点,且PB<PC,PA交BC于E,点F是PC延长线上的点,CF=PB,AB=$\sqrt{13}$,PA=4.
如图,正三角形ABC内接于⊙O,P是BC上的一点,且PB<PC,PA交BC于E,点F是PC延长线上的点,CF=PB,AB=$\sqrt{13}$,PA=4.分析 (1)先根据等边三角形的性质得到AB=AC,再利用圆的内接四边形的性质得∠ACF=∠ABP,于是可根据“SAS”判断△ABP≌△ACF;
(2)先根据等边三角形的性质得到∠ABC=∠ACB=60°,再根据圆周角定理得∠APC=∠ABB=60°,加上∠CAE=∠PAC,于是可判断△ACE∽△APC,然后利用相似比即可得到结论;
(3)先利用AC2=PA•AE计算出AE=$\frac{13}{4}$,则PE=AP-AE=$\frac{3}{4}$,再证△APF为等边三角形,得到PF=PA=4,则有PC+PB=4,接着证明△ABP∽△CEP,得到PB•PC=PE•A=3,然后根据根与系数的关系,可把PB和PC看作方程x2-4x+3=0的两实数解,再解此方程即可得到PB和PC的长.
解答 (1)证明:∵△ABC为等边三角形,
∴AB=AC,
∵四边形ABPC为圆的内接四边形,
∴∠ACF=∠ABP,
在△ABP和△ACF中,
$\left\{\begin{array}{l}{BA=CA}\\{∠ABP=∠ACF}\\{BP=CF}\end{array}\right.$,
∴△ABP≌△ACF;
(2)∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∴∠APC=∠ABB=60°,
∴∠ACE=∠APC,
∵∠CAE=∠PAC,
∴△ACE∽△APC,
∴AE:AC=AC:AP,
∴AC2=PA•AE;
(3)解:∵AC2=PA•AE,AB=AC,
∴AE=$\frac{A{B}^{\;}}{AP}$=$\frac{13}{4}$,
∴PE=AP-AE=4-$\frac{13}{4}$=$\frac{3}{4}$,
∵△ABP≌△ACF,
∴∠APB=∠F=60°,
而∠APC=60°,
∴△APF为等边三角形,
∴PF=PA=4,
∴PC+CF=PC+PB=4,
∵∠BAP=∠PCE,∠APB=∠APC,
∴△ABP∽△CEP,
∴PB:PE=AP:PC,
∴PB•PC=PE•AP=$\frac{3}{4}$×4=3,
∵PB+PC=4,
∴PB和PC可看作方程x2-4x+3=0的两实数解,解此方程得x1=1,x2=3,
∵PB<PC,
∴PB=1,PC=3.
点评 本题考查了圆的综合题:熟练掌握圆周角定理、圆内接四边形的性质和等边三角形的判定与性质;会利用相似三角形证明等积式;会运用根与系数的关系构造一元二次方程.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:解答题
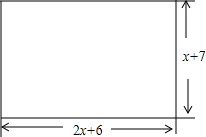 一个工程队要在一块长方形荒地上建造一套简易住房,如图所示,该住房的平面是由长2x+6、宽x+7构成,要求建成:两室、一厅、一厨、一卫,且各房间为长方形或正方形.其中客厅面积为x2+8x+16,厨房面积为3x+6,卫生间面积为x2+3x+2,两个卧室的面积均为3x+9.若墙体所占面积忽略不计,请你根据所学知识,在所给图中设计一套住房的平面结构示意图.(要求:①在图上标出图中各房间的名称;②在图上用含有x的代数式表示图中各房间的边长)
一个工程队要在一块长方形荒地上建造一套简易住房,如图所示,该住房的平面是由长2x+6、宽x+7构成,要求建成:两室、一厅、一厨、一卫,且各房间为长方形或正方形.其中客厅面积为x2+8x+16,厨房面积为3x+6,卫生间面积为x2+3x+2,两个卧室的面积均为3x+9.若墙体所占面积忽略不计,请你根据所学知识,在所给图中设计一套住房的平面结构示意图.(要求:①在图上标出图中各房间的名称;②在图上用含有x的代数式表示图中各房间的边长)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com