
分析 (1)方程左边提取公因式(x+1)即可得到(x+1)(2x+1)=0,进而解两个一元一次方程即可;
(2)把2x2-x-1=0进行因式分解得到(2x+1)(x-1)=0,进而解两个一元一次方程即可.
解答 解:∵2x(x+1)+(x+1)=0,
∴(x+1)(2x+1)=0,
∴x+1=0或2x+1=0,
∴x1=-1,${x_1}=-\frac{1}{2}$;
(2)∵2x2-x-1=0,
∴(2x+1)(x-1)=0,
∴2x+1=0或x-1=0,
∴${x-1}=-\frac{1}{2}$,x2=1.
点评 本题考查了因式分解法解一元二次方程的知识,解答本题的关键是掌握因式分解法解一元二次方程的一般步骤:
①移项,使方程的右边化为零;②将方程的左边分解为两个一次因式的乘积;③令每个因式分别为零,得到两个一元一次方程;④解这两个一元一次方程,它们的解就都是原方程的解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
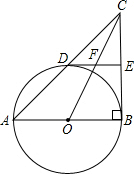 如图,Rt△ABC中,∠ABC=90°,以AB为直径作圆O交AC边于点D,E是边BC的中点,连结OC交DE于点F.
如图,Rt△ABC中,∠ABC=90°,以AB为直径作圆O交AC边于点D,E是边BC的中点,连结OC交DE于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com