
先阅读一段材料:
工人生产零件是按照生产设计图进行操作的.在设计图上,会有一些规定.例如,一个零件的直径大小是![]() ,这里
,这里![]() 表示直径,单位是毫米(mm),它的意思是:零件直径的标准是30 mm,但最大可以是(30+0.05)mm,最小可以是(30-0.04)mm,在这个范围内的产品都是合格的.
表示直径,单位是毫米(mm),它的意思是:零件直径的标准是30 mm,但最大可以是(30+0.05)mm,最小可以是(30-0.04)mm,在这个范围内的产品都是合格的.
根据上述材料完成下列题目:
(1)一种零件,标明的尺寸要求是![]() ,这个零件的合格品最大直径是多少?最小直径是多少?如果零件的直径是49.8 mm,合格吗?
,这个零件的合格品最大直径是多少?最小直径是多少?如果零件的直径是49.8 mm,合格吗?
(2)某种食品的包装质量规定为![]() ,工人在包装时,应把质量控制在什么范围之内?
,工人在包装时,应把质量控制在什么范围之内?
科目:初中数学 来源: 题型:阅读理解
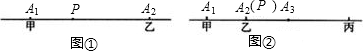
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| 1 |
| 4a |
| 1 |
| 4a |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
查看答案和解析>>
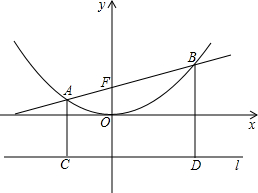
科目:初中数学 来源:2003年全国中考数学试题汇编《二次函数》(04)(解析版) 题型:解答题
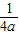 )作对称轴的垂线l,则抛物线上任意一点P到点F(0,
)作对称轴的垂线l,则抛物线上任意一点P到点F(0, )的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0,
)的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0, ).
). x2于A、B、AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图).
x2于A、B、AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图). x2的焦点F的坐标;
x2的焦点F的坐标;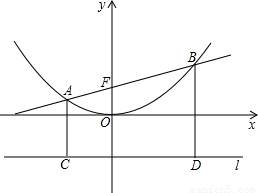
查看答案和解析>>
科目:初中数学 来源:2003年湖北省黄石市中考数学试卷(解析版) 题型:解答题
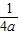 )作对称轴的垂线l,则抛物线上任意一点P到点F(0,
)作对称轴的垂线l,则抛物线上任意一点P到点F(0,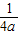 )的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0,
)的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0, ).
). x2于A、B、AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图).
x2于A、B、AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图). x2的焦点F的坐标;
x2的焦点F的坐标;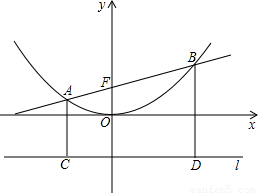
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com