【题目】投掷一枚正六面体骰子，六个面上依次标有
；
，
，
，
，
．
掷得“”的概率是多少？
掷一次“不是”的概率是多少？
掷得数“小于”的概率是多少？
掷得数“小于或等于”的概率是多少？
【答案】（1）
；（2）
；（3）
；（4）
．
【解析】
（1）让向上一面的数字是“6”的情况数除以总情况数6即为所求的概率；
（2）让向上一面的数字是“不是6”的情况数除以总情况数6即为所求的概率；
（3）让向上一面的数字是“小于4”的情况数除以总情况数6即为所求的概率；
（4）让向上一面的数字是“小于或等于4”的情况数除以总情况数6即为所求的概率．
解：
正方体骰子，六个面上依次标有的
，
，
，
，
，
六个数字中，
数字“”只有个，则掷得“”的概率为；
正方体骰子，六个面上依次标有的，，，，，六个数字中，
数字“不是”有，，，，一共个，则掷得“不是”的概率为；
正方体骰子，六个面上依次标有的，，，，，六个数字中，
数字“小于”有，，一共个，则掷得“小于”的概率为
；
正方体骰子，六个面上依次标有的，，，，，六个数字中，
数字“小于或等于”有，，，一共个，则掷得“小于或等于”的概率为
．
ABC考王全优卷系列答案科目：初中数学 来源： 题型：
【题目】如图1，顶角为36°的等腰三角形称为锐角黄金三角形．它的底与腰之比为
≈0.618，记为k.受此启发，八年级数学课题组探究底角为36°的等腰三角形，也称钝角黄金三角形，如图2．
(1)在图1和图2中，若DE=BC，求证：EF=AB；
(2)求钝角黄金三角形底与腰的比值(用含k的式子表示)；
(3)如图3，在钝角黄金三角形ABC中，AD，DE依次分割出钝角黄金三角形△ADC，△ADE．若AB＝1，记△ABC，△ADC，△ADE分别为第1，2，3个钝角黄金三角形，以此类推，求第2020个钝角黄金三角形的周长(用含k的式子表示).
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是二次函数 y＝ax2＋bx＋c(a≠0)的图象的一部分，给出下列命题：①a＋b＋c＝0；②b＞2a；③ax2＋bx＋c＝0的两根分别为－3和1；④a－2b＋c＞0.其中正确的命题是( )
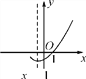
A. ①② B. ②③ C. ①③ D. ①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】佳琪同学在学习了三角形内角和及角平分线定义后经大量的测试实验发现，在一个三角形中，两个内角的角平分线所夹的角只与第三个角的大小有关.
测量数据如下表：
测量 | |||
测量工具 | 量角器 | ||
示意图 |
|
线交于点 | |
测量数据 |
|
| |
第一次 |
|
| |
第二次 |
|
| |
第三次 |
|
| |
第四次 |
|
| |
… | … | ||
（1）通过以上测量数据，请你写出
与
的数量关系：______.
（2）如图，在
中，若
与
的平分线交于点
，则
与存在怎样的数量关系？请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线y=ax2+
x+4的对称轴是直线x=3，且与x轴相交于A，B两点（B点在A点右侧）与y轴交于C点．
（1）求抛物线的解析式和A、B两点的坐标；
（2）若点P是抛物线上B、C两点之间的一个动点（不与B、C重合），则是否存在一点P，使△PBC的面积最大．若存在，请求出△PBC的最大面积；若不存在，试说明理由；
（3）若M是抛物线上任意一点，过点M作y轴的平行线，交直线BC于点N，当MN=3时，求M点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在直角坐标系中，长方形ABCD（每个内角都是90°）的顶点的坐标分别是A（0，m），B（n，0），（m＞n＞0），点E在AD上，AE＝AB，点F在y轴上，OF＝OB，BF的延长线与DA的延长线交于点M，EF与AB交于点N．
（1）试求点E的坐标（用含m，n的式子表示）；
（2）求证：AM＝AN；
（3）若AB＝CD＝12cm，BC＝20cm，动点P从B出发，以2cm/s的速度沿BC向C运动的同时，动点Q从C出发，以vcm/s的速度沿CD向D运动，是否存在这样的v值，使得△ABP与△PQC全等？若存在，请求出v值；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】不透明的袋子中装有
个相同的小球，它们除颜色外无其它差别，把它们分别标号：
、
、
、
随机摸出一个小球后，放回并摇匀，再随机摸出一个，用列表或画树状图的方法求出“两次取的球标号相同”的概率
随机摸出两个小球，直接写出“两次取出的球标号和等于”的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
