
【题目】某果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该果园每棵果树产果![]() (千克),增种果树
(千克),增种果树![]() (棵), 它们之间的函数关系如图所示.
(棵), 它们之间的函数关系如图所示.
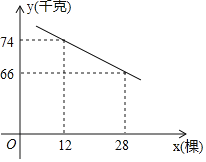
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
科目:初中数学 来源: 题型:
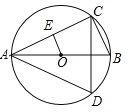
【题目】如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,∠CAB=30°
求:(1)求∠ADC的度数;
(2)如果OE⊥AC,垂足为E,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解市民对“垃圾分类知识”的知晓程度,某数学学习兴趣小组对市民进行随机抽样的问卷调查,调查结果分为“![]() .非常了解”、“
.非常了解”、“![]() .了解”、“
.了解”、“![]() .基本了解”、“
.基本了解”、“![]() .不太了解”四个等级进行统计,并将统计结果绘制成如下两幅不完整的统计图(图1,图2),请根据图中的信息解答下列问题.
.不太了解”四个等级进行统计,并将统计结果绘制成如下两幅不完整的统计图(图1,图2),请根据图中的信息解答下列问题.
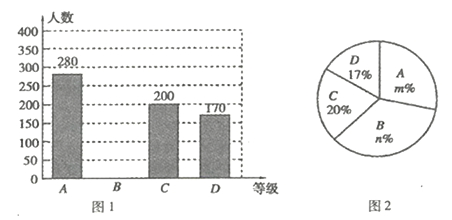
(1)这次调查的市民人数为 人,图2中, ![]() ;
;
(2)补全图1中的条形统计图;
(3)在图2中的扇形统计图中,求“![]() .基本了解”所在扇形的圆心角度数;
.基本了解”所在扇形的圆心角度数;
(4)据统计,2018年该市约有市民500万人,那么根据抽样调查的结果,可估计对“垃圾分类知识”的知晓程度为“![]() .不太了解”的市民约有多少万人?
.不太了解”的市民约有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
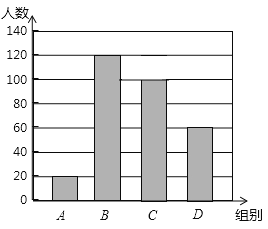
【题目】国家规定,中、小学生每天在校体育活动时间不低于1h.为此,某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h.
请根据上述信息解答下列问题:
(1)本次调查数据的众数落在 组内,中位数落在 组内;
(2)该辖区约有18000名初中学生,请你估计其中达到国家规定体育活动时间的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,同学们利用所学知识去测量海平面上一个浮标到海岸线的距离. 在一笔直的海岸线l上有A、B两个观测站,A在B的正东方向,小宇同学在A处观测得浮标在北偏西60°的方向,小英同学在距点A处60米远的B点测得浮标在北偏西45°的方向,求浮标C到海岸线l的距离(结果精确到0.01 m).

查看答案和解析>>
科目:初中数学 来源: 题型:
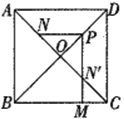
【题目】如图,在正方形ABCD中,AB=4,AC与![]() 相交于点O,N是AO的中点,点M在BC边上,P是OD的中点,过点P作PM⊥BC于点M,交
相交于点O,N是AO的中点,点M在BC边上,P是OD的中点,过点P作PM⊥BC于点M,交![]() 于点N′,则PN-MN′的值为( )
于点N′,则PN-MN′的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
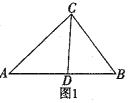
(1)如图1,在△ABC中,∠A=40°,∠B=60°,当∠BCD=40°时,证明:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD是以AC为底边的等腰三角形,求∠ACB的度数.
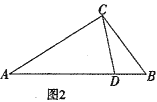
(3)如图2,在△ABC中,AC=2,BC=2,CD是△ABC的完美分割线,△ACD是以CD为底边的等腰三角形,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
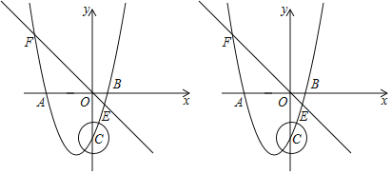
【题目】如图,抛物线y=mx2+nx﹣3(m≠0)与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C,直线y=﹣x与该抛物线交于E,F两点.
(1)求点C坐标及抛物线的解析式.
(2)P是直线EF下方抛物线上的一个动点,作PH⊥EF于点H,求PH的最大值.
(3)以点C为圆心,1为半径作圆,⊙C上是否存在点D,使得△BCD是以CD为直角边的直角三角形?若存在,直接写出D点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4,∠ADN=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N.连接MD、AN,
(1)求证:四边形AMDN是平行四边形;
(2)填空:
①当AM的值为_____时,四边形AMON是矩形;
②当AM的值为______时,四边形AMDN是菱形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com