
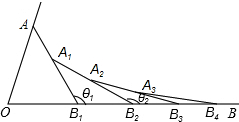
 如图,已知∠AOB=α,在射线OA、OB上分别取点OA=OB1,连结AB1,在B1A、B1B上分别取点A1、B2,使B1B2=B1A1,连结A1B1…按此规律上去,记∠A1B1B2=θ1,∠A2B2B3=θ2,…,∠AnBnBn+1=θn,则:
如图,已知∠AOB=α,在射线OA、OB上分别取点OA=OB1,连结AB1,在B1A、B1B上分别取点A1、B2,使B1B2=B1A1,连结A1B1…按此规律上去,记∠A1B1B2=θ1,∠A2B2B3=θ2,…,∠AnBnBn+1=θn,则:分析 根据等腰三角形两底角相等用α表示出∠AB1O,再根据邻补角的定义表示出θ1,同理表示出θ2,θ3,…,θn.
解答 解:∵OA=OB1,
∴∠AB1O=$\frac{1}{2}$(180°-α),
∴θ1=180°-$\frac{1}{2}$(180°-α)=$\frac{180°+α}{2}$,
∵A1B1=B1B2,
∴∠A1B2B1=$\frac{1}{2}$(180°-$\frac{180°+α}{2}$)=$\frac{180°-α}{4}$,
∴θ2=180°-∠A1B2B1=180°-$\frac{180°-α}{4}$=$\frac{3×180°+α}{4}$,
同理可得:θ3=$\frac{7×180°+α}{8}$,
…,
∴θn=$\frac{({2}^{n}-1)•180°+α}{{2}^{n}}$.
点评 此题主要考查学生对等腰三角形性质和三角形内角和定理的理解和掌握,解答此题的关键是总结归纳出规律.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,A、B之间是一座山,一条高速公路要通过A、B两点,在A地测得公路走向是北偏东70°32′.如果A、B两地同时开工,则:
如图,A、B之间是一座山,一条高速公路要通过A、B两点,在A地测得公路走向是北偏东70°32′.如果A、B两地同时开工,则:查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 6cm3以上,8cm3以下 | B. | 8cm3以上,10cm3以下 | ||
| C. | 10cm3以上,12cm3以下 | D. | 12cm3以上,14cm3以下 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com