练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

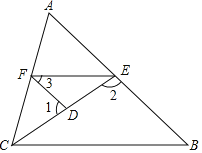
    【题目】如图，已知∠1，∠2互为补角，且∠3＝∠B．

    （1）求证：EF∥BC；

    （2）若CE平分∠ACB，且∠1＝80°，∠3＝45°，求∠AFE的度数．

    【答案】（1）证明见解析；（2）∠AFE=70°．

    【解析】

    （1）先证DF∥AB，推出∠3＝∠AEF，进而得∠B＝∠AEF，得出FE∥BC即可；

    （2）求出∠FED＝80°﹣45°＝35°，根据平行线性质求出∠BCE＝∠FED＝35°，求出∠ACB＝2∠BCE＝70°，根据平行线性质，即可求解．

    （1）∵∠1+∠FDE＝180°，∠1+∠2=180°，

    ∴∠2＝∠FDE，

    ∴DF∥AB，

    ∴∠3＝∠AEF，

    ∵∠3＝∠B，

    ∴∠B＝∠AEF，

    ∴FE∥BC；

    （2）∵∠1＝80°，∠3＝45°，

    ∴∠FED＝80°﹣45°＝35°，

    ∵EF∥BC，

    ∴∠BCE＝∠FED＝35°，

    ∵CE平分∠ACB，

    ∴∠ACB＝2∠BCE＝70°，

    ∴∠AFE＝∠ACB＝70°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】直线AB∥CD，点P在其所在平面上，且不在直线AB，CD，AC上，设∠PAB=α，∠PCD=β，∠APC=γ(α，β，γ，均不大于180°，且不小于0°)．

    （1）如图1，当点P在两条平行直线AB，CD之间、直线AC的右边时试确定α，β，γ的数量关系；

    （2）如图2，当点P在直线AB的上面、直线AC的右边时试确定α，β，γ的数量关系；

    （3）α，β，γ的数量关系除了上面的两种关系之外，还有其他的数量关系，请直接写出这些．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点 P 是∠AOB 内部一定点

    （1）若∠AOB＝50°，作点 P 关于 OA 的对称点 P1，作点 P 关于 OB 的对称点 P2，连 OP1、OP2，则∠P1OP2＝___.

    （2）若∠AOB＝α，点 C、D 分别在射线 OA、OB 上移动，当△PCD 的周长最小时，则∠CPD＝___（用 α 的代数式表示）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，A（5，0），B（0，5）.

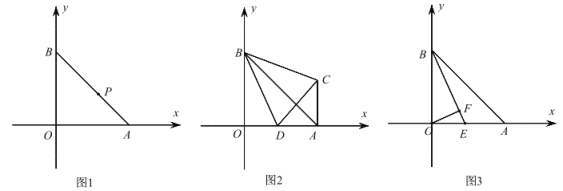
    （1）如图 1，P 是 AB 上一点且，求 P 点坐标；

    （2）如图 2，D 为 OA 上一点，AC∥OB 且∠CBO＝∠DCB，求∠CBD 的度数；

    （3）如图 3，E 为 OA 上一点，OF⊥BE 于 F，若∠BEO＝45°＋∠EOF，求的值

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】完成下面的证明

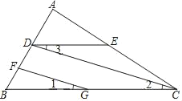
    （1）如图，FG∥CD，∠1＝∠3，∠B＝50°，求∠BDE的度数．

    解：∵FG∥CD（已知）

    ∴∠2＝　 　

    又∵∠1＝∠3，

    ∴∠3＝∠2（等量代换）

    ∴BC∥　 　

    ∴∠B+　 　＝180°　 　

    又∵∠B＝50°

    ∴∠BDE＝　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系中，已知A（a，0），B（b，3），C（4，0），且满足（a+b）2+|a﹣b+6|=0，线段AB交y轴于F点．

    （1）求点A、B的坐标；

    （2）点D为y轴正半轴上一点，若ED∥AB，且AM，DM分别平分∠CAB，∠ODE，如图 2，求∠AMD的度数；

    （3）如图 3，（也可以利用图 1）①求点F的坐标；②坐标轴上是否存在点P，使得△ABP和△ABC的面积相等？若存在，求出P点坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

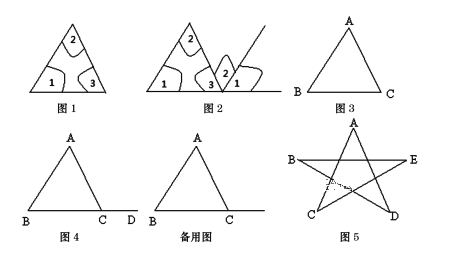
    【题目】下列是某初一数学兴趣小组探究三角形内角和的过程，请根据他们的探究过程，结合所学知识，解答下列问题.兴趣小组将图1△ABC三个内角剪拼成图2，由此得△ABC三个内角的和为180度.

    （1）请利用图3证明上述结论.

    （2）三角形的一条边与另一条边的反向延长线组成的角，叫做三角形的外角.

    如图4，点D为BC延长线上一点，则∠ACD为△ABC的一个外角.

    ①请探究出∠ACD与∠A、∠B的关系，并直接填空：∠ACD=______.

    ②如图5是一个五角星，请利用上述结论求∠A+∠B＋∠C＋∠D＋∠E的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC为等边三角形，D为边BA延长线上一点，连接CD，以CD为一边作等边三角形CDE，连接AE．

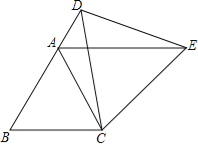
    （1）求证：△CBD≌△CAE．

    （2）判断AE与BC的位置关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义一种新运算“♀”，观察下列运算：

    （+5）♀（+14）=+19，

    ♀=+20,

    ,

    ，

    ，

    (+13)♀0=+13．

    （1）请你认真思考上述运算，归纳运算“♀”的法则．

    两数进行运算“♀”时，同号______，异号_________，特别地，0和任何数进行运算“♀”，或任何数和0进行运算“♀”，结果都为_______．

    （2）计算：♀[0♀]．

    查看答案和解析>>

    同步练习册答案